题目内容
某计算机程序每运行一次都随机出现一个二进制的六位数N=n1,n2,n3,n4,n5,n6,其中N的各位数中,n1=n6=1,nk(k=2,3,4,5)出现0的概率为| 2 |
| 3 |
| 1 |
| 3 |
分析:k=2,3,4,5时,出现0的概率为
,出现1的概率为
,n2,n3,n4,n5 中0的个数服从二项分布,代公式求解即可.
| 2 |
| 3 |
| 1 |
| 3 |
解答:解:ξ的可能取值是2,3,4,5,6.
∵n1=n6=1,
∴P(ξ=2)=
(
)4=
,P(ξ=3)=
•(
)3=
,P(ξ=4)=
(
)2•(
)2=
,P(ξ=5)=
(
)3•
=
,P(ξ=6)=
(
)4=
.
∴ξ的分布列为:
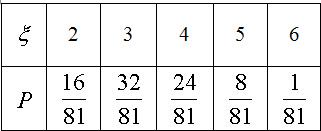
∴ξ的数学期望为Eξ=2×
+3×
+4×
+5×
+6×
=
.
∵n1=n6=1,
∴P(ξ=2)=
| C | 0 4 |
| 2 |
| 3 |
| 16 |
| 81 |
| C | 1 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 32 |
| 81 |
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
| C | 3 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 81 |
| C | 4 4 |
| 1 |
| 3 |
| 1 |
| 81 |
∴ξ的分布列为:

∴ξ的数学期望为Eξ=2×
| 16 |
| 81 |
| 32 |
| 81 |
| 24 |
| 81 |
| 8 |
| 81 |
| 1 |
| 81 |
| 10 |
| 3 |
点评:本题主要考查随机变量的分布列及其数学期望等基础知识,考查运算求解能力.重点考查二项分布的求解.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
某计算机程序每运行一次都随机出现一个五位的二进制数A= ,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为
,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为
,出现1的概率为
.记X=a2+a3+a4+a5,当程序运行一次时,X的数学期望Eξ=( )
 ,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为
,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为| 1 |
| 3 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 ,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为
,其中A的各位数中,a1=1,ak(k=2,3,4,5)出现0的概率为