题目内容
设椭圆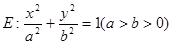 的离心率
的离心率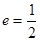 ,
,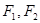 是其左右焦点,点
是其左右焦点,点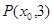 是直线
是直线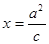 (其中
(其中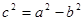 )上一点,且直线
)上一点,且直线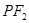 的倾斜角为
的倾斜角为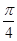 .
.
(Ⅰ)求椭圆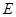 的方程;
的方程;
(Ⅱ)若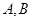 是椭圆
是椭圆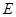 上两点,满足
上两点,满足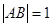 ,求
,求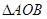 (
(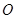 为坐标原点)面积的最小值.
为坐标原点)面积的最小值.
【答案】
(Ⅰ)  ;(Ⅱ)
;(Ⅱ)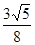 .
.
【解析】
试题分析:(Ⅰ) 根据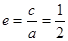 及
及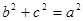 得
得 ;(Ⅱ)分斜率存在和不存在进行讨论,当斜率不存在,易求得
;(Ⅱ)分斜率存在和不存在进行讨论,当斜率不存在,易求得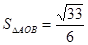 ,当斜率存在时,利用弦长公式表示出
,当斜率存在时,利用弦长公式表示出 再表示出面积
再表示出面积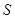 ,得
,得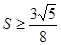 ,从而
,从而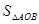 的最小值为
的最小值为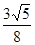
试题解析:(Ⅰ)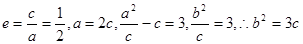
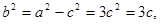 则
则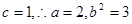 ,故
,故
(Ⅱ)当直线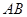 的斜率不存在时,可设
的斜率不存在时,可设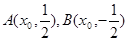 代入椭圆得
代入椭圆得
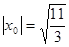 ,此时,
,此时,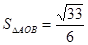 , 当直线
, 当直线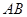 的斜率存在时,设
的斜率存在时,设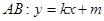 代入椭圆得:
代入椭圆得:
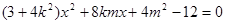 , 设
, 设
则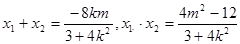
由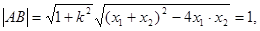 得:
得: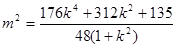
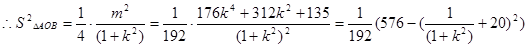
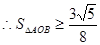
当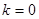 时,取等号,又
时,取等号,又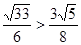 ,故
,故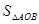 的最小值为
的最小值为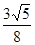 .
.
考点:直线与椭圆的位置关系综合应用.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
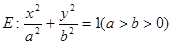 的离心率
的离心率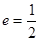 ,
,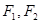 是其左右焦点,点
是其左右焦点,点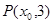 是直线
是直线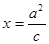 (其中
(其中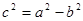 )上一点,且直线
)上一点,且直线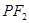 的倾斜角为
的倾斜角为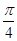 .
.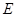 的方程;
的方程;
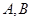 是椭圆
是椭圆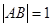 ,求
,求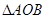 (
(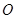 为坐标原点)面积的最小值.
为坐标原点)面积的最小值.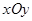 中,已知椭圆
中,已知椭圆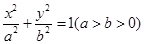 的离心率为
的离心率为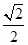 ,其焦点在圆
,其焦点在圆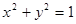 上.
上.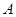 、
、 、
、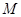 是椭圆上的三点(异于椭圆顶点),且存在锐角
是椭圆上的三点(异于椭圆顶点),且存在锐角 ,使
,使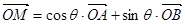 .
. 与
与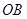 的斜率的乘积;
的斜率的乘积;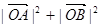 的值.
的值.