题目内容
已知双曲线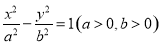 的离心率为
的离心率为 ,左顶点到一条渐近线的距离为
,左顶点到一条渐近线的距离为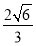 ,则该双曲线的标准方程为( )
,则该双曲线的标准方程为( )
A. B.
B.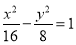
C.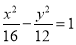 D.
D.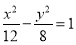
练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
题目内容
已知双曲线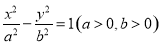 的离心率为
的离心率为 ,左顶点到一条渐近线的距离为
,左顶点到一条渐近线的距离为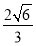 ,则该双曲线的标准方程为( )
,则该双曲线的标准方程为( )
A. B.
B.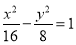
C.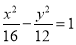 D.
D.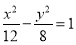
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案