题目内容
若复数z=（a2 +2a－3）+（a－l）i为纯虚数（i为虚数单位），则实数a的值为
| A．－3 | B．－3或1 | C．3或－1 | D．1 |
A
解析试题分析：复数z=（a2 +2a－3）+（a－l）i为纯虚数（i为虚数单位），则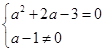
，解得
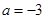。故选A。
考点：复数的概念
点评：在复数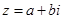
中，a是实部，b是虚部，i是虚数单位。要得到复数的实部和虚部，需将复数变成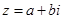的形式。
练习册系列答案
名校课堂系列答案
相关题目
设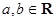
，
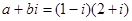（i为虚数单位），则
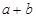的值为( )
| A．0 | B．2 | C．3 | D．4 |
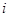是虚数单位，若集合
=
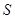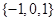，则（ ）
A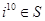． | B． | C． | D． ∈ |
在复平面内，复数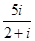
的对应点位于 （ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
如果复数(m2+i)(1+mi)是实数，则实数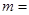
( )
| A．1 | B．-1 | C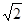． | D．- |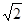
复数
满足
，则
A． | B． | C． | D． |
已知复数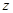
满足
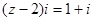，那么复数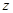的虚部为
| A．1 | B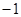． | C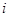． | D． |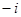
关于复数的命题：
（1）复数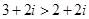
；（2）复数
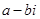的模为
；
（3）在复平面内,纯虚数与
轴上的点一一对应，其中真命题的个数是（ ）．
| A．0个 | B．1个 | C．2个 | D．3个 |
复数
= （ ）
A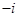． | B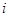． | C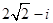． | D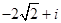． |