题目内容
（09年东城区示范校质检一）（13分）
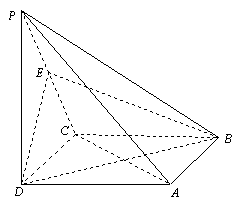
如图，在四棱锥
中，底面ABCD是正方形，侧棱
底面ABCD，
，E是PC的中点.
（1）证明 
平面
；
（2）求EB与底面ABCD所成的角的正切值.
|
解析：（I）证明：连结AC，AC交BD于O.连结EO.
底面ABCD是正方形，
点O是AC的中点
在
中，EO是中位线，
. ………………3分
而
平面EDB且
平面EDB，
所以
平面EDB. ………………5分
|
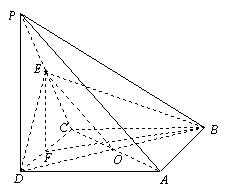
（II）解：
作
交DC于F.连结BF.设正方形
ABCD的边长为
.
底面ABCD，
为DC的中点.
底面ABCD，BF为BE在底面ABCD
内的射影，
故
为直线EB与底面ABCD所成的角.
………………8分
在
中，
在
中，
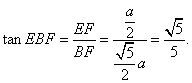
所以EB与底面ABCD所成的角的正切值为
…………………………13分
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
的定义域为全体R，当x<0时，
，且对任意的实数x，y∈R，有
成立，数列
满足
，且
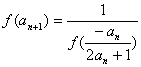（n∈N*）
对一切n∈N*均成立，求k的
上的奇函数，当
时，
（a为实数）．
时，f(x)的解析式；
上是增函数，求a的取值范围；
中，角
的对边分别为
，且
. 
的值；
，
，求
和
．
时都取得极值
的单调区间；
的取值范围。