题目内容
一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如下图所示,则该几何体的俯视图为（ ）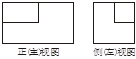
C
解析试题分析：由正（主）视图可知去掉的长方体在正对视线的方向，从侧（左）视图可以看出去掉的长方体在原长方体的左侧，由以上各视图的描述可知其俯视图符合C选项
考点：本题考查了三视图的运用
点评：此类问题主要运用几何体的三视图之间的关系，要注意记忆和理解“长对正、高平齐、宽相等”的含义
练习册系列答案
阅读快车系列答案
相关题目
如图是水平放置的平面图形的斜二测直观图，其原来平面图形面积是（ ）
A．2 | B．4 | C．4 | D．8 |
一个空间几何体的三视图如图所示，则该几何体的表面积为（ ）
| A．48 | B．32+8 | C．48+8 | D．80 |
一个几何体的三视图如图所示，则这个几何体的体积为
A． | B．  | C． | D． |
已知某几何体的三视图如图所示，则该几何体的体积为（ ）
A． | B．3π | C． | D．6π |
、
、
、
四点，若
，则四面体
的体积的取值范围是
在一个几何体的三视图中，正视图和俯视图如下图所示，则该几何体的体积为（ ）
A． cm3（ | B． cm3 | C． cm3 | D． cm3 |
设
是三个不重合的平面，l是直线，给出下列命题：
①若
，则
； ②若
③若l上存在两点到
的距离相等，则
； ④若
其中正确的命题是（ ）
| A．①② | B．②③ | C．②④ | D．③④ |