题目内容
设f(x)=
(其中e为自然对数的底数),则
f(x)dx的值为( )
|
| ∫ | e2 0 |
分析:把积分区间[0,e2]分为[0,1]和[1,e2],然后在这两个区间上分别积分即可.
解答:解:
f(x)dx=
x2dx+
dx=
x3
+lnx
=
+2=
.
故选C.
| ∫ | e2 0 |
| ∫ | 1 0 |
| ∫ | e2 1 |
| 1 |
| x |
| 1 |
| 3 |
| | | 1 0 |
| | | e2 1 |
| 1 |
| 3 |
| 7 |
| 3 |
故选C.
点评:本题考查了分段函数的定积分,分段函数在不同区间上的表达式不同,所以要分区间积分.

练习册系列答案
相关题目
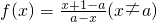
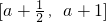 时,求f(x)的值域;
时,求f(x)的值域;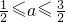 ,求g(x)的最小值.
,求g(x)的最小值.