题目内容
已知正项数列{an}的前n和为Sn，且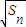
是
与（an+1）2的等比中项．（1）求证：数列{an}是等差数列；
（2）若
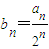，数列{bn}的前n项和为Tn，求Tn．
【答案】分析：（1）要证明数列{an}为等差数列，需证明an-an-1=d，由已知条件可得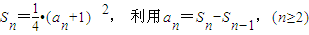
（2）
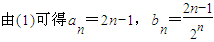用错位相减求和
解答：解：（1）由题意可知，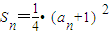
当n≥2，
整理可得（an-1）2=（an-1+1）2=（an-1+1）2
∵an＞0∴an-an-1=2
n=1，由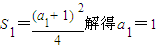
数列an以1为首项，以2为公差的等差数列
（2）由（1）可得an=1+2（n-1）=2n-1
∴
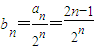
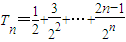①
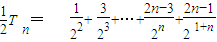②
∴
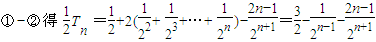
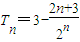
点评：本题重点考查利用递推公式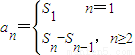
转化数列an+1与an的递推关系、等差数列的证明及错位相减求数列的和，求解的关键是要把握递推公式的转化．
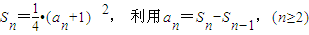
（2）
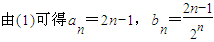用错位相减求和解答：解：（1）由题意可知，
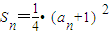
当n≥2，
整理可得（an-1）2=（an-1+1）2=（an-1+1）2
∵an＞0∴an-an-1=2
n=1，由
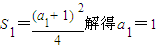
数列an以1为首项，以2为公差的等差数列
（2）由（1）可得an=1+2（n-1）=2n-1
∴
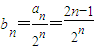
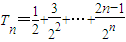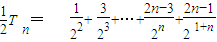①②∴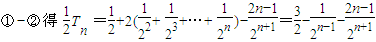
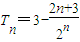
点评：本题重点考查利用递推公式
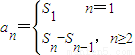转化数列an+1与an的递推关系、等差数列的证明及错位相减求数列的和，求解的关键是要把握递推公式的转化． 
练习册系列答案
相关题目