题目内容
已知函数 在x=1处取到极值2.
在x=1处取到极值2.(Ⅰ)求f(x)的解析式;
(Ⅱ)设函数
 .若对任意的x1∈R,总存在x2∈[1,e],使得
.若对任意的x1∈R,总存在x2∈[1,e],使得 ,求实数a的取值范围.
,求实数a的取值范围.
【答案】分析:(Ⅰ)利用函数的求导公式计算函数的导数,根据函数在x=1处取到极值得出函数在x=1处的导数为0,再把x=2代入函数,联立两式求出m,n的值即可.
已知函数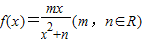 在x=1处取到极值2.
在x=1处取到极值2.
(Ⅱ)由(Ⅰ)知f(x)的定义域为R,且f(-x)=-f(x).故f(x)为奇函数.f(0)=0,x>0时,f(x)>0,f(x)=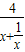 ≤2.当且仅当x=1时取“=”.
≤2.当且仅当x=1时取“=”.
故f(x)的值域为[-2,2].从而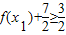 .依题意有
.依题意有 (7分)
(7分)
解答:解:(Ⅰ)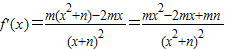 (2分)
(2分)
根据题意,f(x)=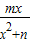 ,
,
f′(x)=-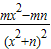 ;
;
由f(x)在x=1处取到极值2,故f′(1)=0,f(1)=2即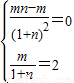 ,
,
解得m=4,n=1,经检验,此时f(x)在x=1处取得极值.故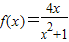 (4分)
(4分)
(Ⅱ)由(Ⅰ)知f(x)的定义域为R,且f(-x)=-f(x).故f(x)为奇函数.f(0)=0,x>0时,f(x)>0,f(x)=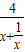 ≤2.当且仅当x=1时取“=”.
≤2.当且仅当x=1时取“=”.
故f(x)的值域为[-2,2].从而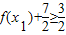 .依题意有
.依题意有 (7分)
(7分)
函数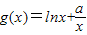 的定义域为(0,+∞),
的定义域为(0,+∞),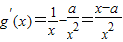 (8分)
(8分)
①当a≤1时,g′(x)>0函数g(x)在[1,e]上单调递增,其最小值为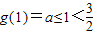 合题意;
合题意;
②当1<a<e时,函数g(x)在[1,a)上有g′(x)<0,单调递减,在(a,e]上有g′(x)>0,单调递增,所以函数g(x)最小值为f(a)=lna+1,由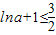 ,得
,得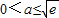 .从而知
.从而知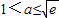 符合题意.
符合题意.
③当a≥e时,显然函数g(x)在[1,e]上单调递减,其最小值为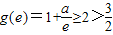 ,不合题意(11分)综上所述,a的取值范围为
,不合题意(11分)综上所述,a的取值范围为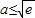 (12分)
(12分)
点评:该题考查函数的求导,以及函数极值的应用,考查一个函数小于零一个函数时,小于它的最小值.要会利用函数的导数判断函数的单调性.
已知函数
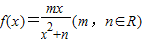 在x=1处取到极值2.
在x=1处取到极值2.(Ⅱ)由(Ⅰ)知f(x)的定义域为R,且f(-x)=-f(x).故f(x)为奇函数.f(0)=0,x>0时,f(x)>0,f(x)=
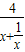 ≤2.当且仅当x=1时取“=”.
≤2.当且仅当x=1时取“=”.故f(x)的值域为[-2,2].从而
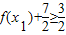 .依题意有
.依题意有 (7分)
(7分)解答:解:(Ⅰ)
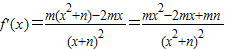 (2分)
(2分)根据题意,f(x)=
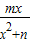 ,
,f′(x)=-
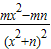 ;
;由f(x)在x=1处取到极值2,故f′(1)=0,f(1)=2即
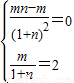 ,
,解得m=4,n=1,经检验,此时f(x)在x=1处取得极值.故
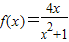 (4分)
(4分)(Ⅱ)由(Ⅰ)知f(x)的定义域为R,且f(-x)=-f(x).故f(x)为奇函数.f(0)=0,x>0时,f(x)>0,f(x)=
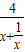 ≤2.当且仅当x=1时取“=”.
≤2.当且仅当x=1时取“=”.故f(x)的值域为[-2,2].从而
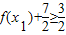 .依题意有
.依题意有 (7分)
(7分)函数
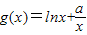 的定义域为(0,+∞),
的定义域为(0,+∞),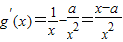 (8分)
(8分)①当a≤1时,g′(x)>0函数g(x)在[1,e]上单调递增,其最小值为
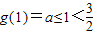 合题意;
合题意;②当1<a<e时,函数g(x)在[1,a)上有g′(x)<0,单调递减,在(a,e]上有g′(x)>0,单调递增,所以函数g(x)最小值为f(a)=lna+1,由
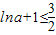 ,得
,得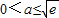 .从而知
.从而知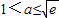 符合题意.
符合题意.③当a≥e时,显然函数g(x)在[1,e]上单调递减,其最小值为
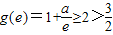 ,不合题意(11分)综上所述,a的取值范围为
,不合题意(11分)综上所述,a的取值范围为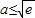 (12分)
(12分)点评:该题考查函数的求导,以及函数极值的应用,考查一个函数小于零一个函数时,小于它的最小值.要会利用函数的导数判断函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在x=1处取到极值2
在x=1处取到极值2 ,总存在唯一的
,总存在唯一的 ,使得g(x2)=f(x1),求实数a的取值范围.
,使得g(x2)=f(x1),求实数a的取值范围. 在x=1处取到极值2
在x=1处取到极值2 ,总存在唯一的
,总存在唯一的 ,使得g(x2)=f(x1),求实数a的取值范围.
,使得g(x2)=f(x1),求实数a的取值范围.