题目内容
已知函数 若
若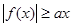 ,则
,则 的取值范围是 .
的取值范围是 .
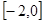
解析试题分析:当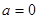 时,
时,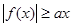 显然成立;
显然成立;
当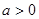 时,若
时,若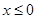 ,
,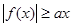 显然成立,所以只要
显然成立,所以只要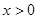 时,
时, 成立即可,比较对数与一次函数的增长速度,不存在
成立即可,比较对数与一次函数的增长速度,不存在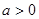 使
使 在
在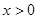 恒成立;
恒成立;
当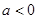 时,若
时,若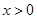 ,
,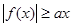 显然成立,所以只要
显然成立,所以只要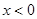 时
时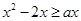 ,解得
,解得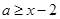 ,∴
,∴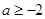 ,
,
∴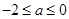 .
.
考点:不等式,对数不等式的解法.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
题目内容
已知函数 若
若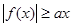 ,则
,则 的取值范围是 .
的取值范围是 .
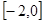
解析试题分析:当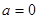 时,
时,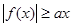 显然成立;
显然成立;
当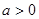 时,若
时,若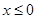 ,
,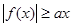 显然成立,所以只要
显然成立,所以只要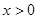 时,
时, 成立即可,比较对数与一次函数的增长速度,不存在
成立即可,比较对数与一次函数的增长速度,不存在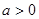 使
使 在
在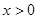 恒成立;
恒成立;
当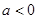 时,若
时,若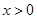 ,
,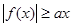 显然成立,所以只要
显然成立,所以只要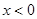 时
时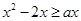 ,解得
,解得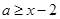 ,∴
,∴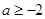 ,
,
∴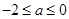 .
.
考点:不等式,对数不等式的解法.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案