题目内容
若函数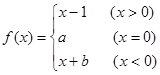 是奇函数,则a+b= 。
是奇函数,则a+b= 。
1
解析试题分析:有函数解析式可得:其为定义在实数集R上的奇函数.
所以有:f(0)=0,∴a=0,
又∵f(1)=-f(-1)
∴0=-[(-1)+b]⇒b=1.
∴a+b=1.
故答案为:1.
考点:本题主要考查了奇函数的定义和性质的运用。
点评:解决该试题的关键是奇函数的性质.当一个函数是定义在实数集R上的奇函数时,一定有f(0)=0.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
题目内容
若函数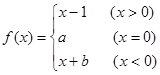 是奇函数,则a+b= 。
是奇函数,则a+b= 。
1
解析试题分析:有函数解析式可得:其为定义在实数集R上的奇函数.
所以有:f(0)=0,∴a=0,
又∵f(1)=-f(-1)
∴0=-[(-1)+b]⇒b=1.
∴a+b=1.
故答案为:1.
考点:本题主要考查了奇函数的定义和性质的运用。
点评:解决该试题的关键是奇函数的性质.当一个函数是定义在实数集R上的奇函数时,一定有f(0)=0.

 53随堂测系列答案
53随堂测系列答案