题目内容
关于 的函数
的函数 ,有下列结论:
,有下列结论:
①、该函数的定义域是 ; ②、该函数是奇函数;
; ②、该函数是奇函数;
③、该函数的最小值为 ;
;
④、当 时
时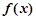 为增函数,当
为增函数,当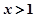 时
时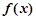 为减函数;
为减函数;
其中,所有正确结论的序号是 。
①④
解析试题分析: :①函数f(x)的定义域是(0,+∞),令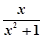 >0,解得x>0,故定义域是(0,+∞),命题正确;
>0,解得x>0,故定义域是(0,+∞),命题正确;
②函数f(x)是奇函数,由①知,定义域不关于原点对称,故不是奇函数,命题不正确;
③函数f(x)的最大值为-lg2,因为f(x)= 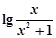 =lg
=lg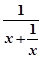 ≤lg
≤lg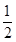 =-lg2,最大值是-lg2,故命题不正确;
=-lg2,最大值是-lg2,故命题不正确;
④当0<x<1时,函数f(x)是增函数;当x>1时,函数f(x)是减函数,命题正确,因为f′(x)=lg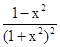 ,令导数大于0,可解得0<x<1,令导数大于0,得x>1,故命题正确.综上,①④正确,故答案为:①④
,令导数大于0,可解得0<x<1,令导数大于0,得x>1,故命题正确.综上,①④正确,故答案为:①④
考点:本题主要考查了函数定义域、最值、单调性和奇偶性,同时考查了推理论证的能力以及计算论证的能力,属于中档题.
点评:解决该试题的关键是①根据对数函数的真数大于0,建立关系式解之验证定义域即可;②函数f(x)是奇函数,利用奇函数的定义进行判断;③函数f(x)的最大值为-lg2,利用基本不等式与对数的运算性质求出最值;④求出导数,解出单调区间,验证即可.

练习册系列答案
相关题目
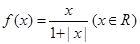 时,分别给出下面几个结论:
时,分别给出下面几个结论: 对
对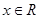 恒成立; ②函数
恒成立; ②函数 的值域为
的值域为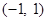 ;
;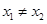 ,则一定有
,则一定有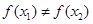 ; ④函数
; ④函数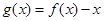 在
在 上有三个零点。 其中正确结论的序号有____________.
上有三个零点。 其中正确结论的序号有____________.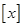 表示不超过
表示不超过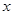 的最大整数,定义函数
的最大整数,定义函数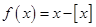 .则下列结论中正确的有
.则下列结论中正确的有 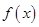 的值域为
的值域为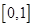 ②方程
②方程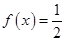 有无数个解
有无数个解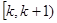
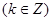 上是增函数
上是增函数 ,若函数
,若函数 有3个零点,则实数
有3个零点,则实数 的取值范围是 .
的取值范围是 .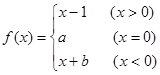 是奇函数,则a+b= 。
是奇函数,则a+b= 。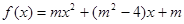 是偶函数,
是偶函数,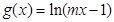 在
在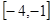 内单调递减,则实数
内单调递减,则实数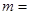 。
。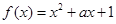 是偶函数,则函数
是偶函数,则函数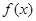 的最小值为 .
的最小值为 .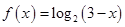 ,则函数
,则函数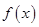 的定义域是______.(用区间表示)
的定义域是______.(用区间表示)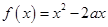 在
在 上增函数,则
上增函数,则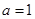 ;
;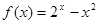 只有两个零点;
只有两个零点;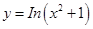 的值域是
的值域是 ;
;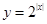 的最小值是1;
的最小值是1;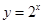 与
与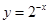 的图像关于
的图像关于 轴对称。
轴对称。