题目内容
6.已知集合M={y|y=x2,x∈R},N={y|x2+$\frac{{y}^{2}}{2}$=1,x∈R},则M∩N=[0,1].分析 求出集合M,N,结合集合的交集运算定义,可得答案.
解答 解:∵集合M={y|y=x2,x∈R}=[0,+∞),
N={y|x2+$\frac{{y}^{2}}{2}$=1,x∈R}=[-1,1],
∴M∩N=[0,1],
故答案为:[0,1]
点评 本题考查的知识点是集合的交集,交集,补集运算,难度不大,属于基础题.

练习册系列答案
相关题目
16.函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-2ax+4a(x<1)}\\{(a-3)x+4a(x≥1)}\end{array}\right.$,满足对任意x1≠x2,都有 $\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,则a的取值范围是( )
| A. | (0,$\frac{3}{4}$) | B. | (0,$\frac{3}{4}$] | C. | (0,1) | D. | [1,$\frac{4}{3}$] |
17.在锐角△ABC中,已知AB=2,∠B=2∠C,则AC的取值范围是( )
| A. | (2$\sqrt{2}$,2$\sqrt{3}$) | B. | (2,2$\sqrt{2}$) | C. | (2$\sqrt{2}$,4) | D. | (2,2$\sqrt{3}$) |
14.在等差数列{an}中,若3(a4+a6)+2(a7+a9+a11)=24,则此数列的前13项之和为( )
| A. | 13 | B. | 26 | C. | 52 | D. | 156 |
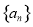 的前
的前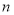 项和
项和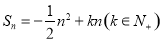 ,且
,且 的最大值为8.
的最大值为8.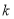 ,并求
,并求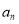 ;
;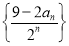 的前
的前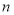 项和
项和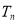 .
.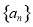 中,
中,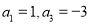 ,则
,则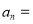 ____________.
____________.