题目内容
已知矩阵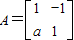 ,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3).
,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3).(1)求实数a的值;
(2)求矩阵A的特征值.
【答案】分析:(1)根据点P在矩阵A的变化下得到的点P′(0,-3),写出题目的关系式,列出关于a的等式,解方程即可.
(2)写出矩阵的特征多项式,令多项式等于0,得到矩阵的特征值,对于两个特征值分别解二元一次方程,得到矩阵A的属于特征值-1的一个特征向量和矩阵A的属于特征值3的一个特征向量.
解答:解:(1)由:(1)由
 =
= ,
,
得a+1=-3,则a=-4(3分)
(2)由(1)知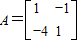 ,
,
所以,由F(λ)=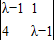 得:λ1=-1,λ2=3(7分)
得:λ1=-1,λ2=3(7分)
λ1=-1时,由-2x+y=0得:y=-2x取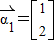
λ2=3时,由2x+y=0得:y=-2x,取 .(9分)
.(9分)
所以,A的特征值为-1或3.
属于-1的一个特征向量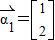 ,
,
属于3的一个特征向量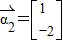 (10分)
(10分)
点评:本题考查二阶矩阵,考查二阶矩阵的特征值的求法,考查二阶矩阵的特征向量的求法,因为是高等数学的内容,考查的比较简单,是一个中档题.
(2)写出矩阵的特征多项式,令多项式等于0,得到矩阵的特征值,对于两个特征值分别解二元一次方程,得到矩阵A的属于特征值-1的一个特征向量和矩阵A的属于特征值3的一个特征向量.
解答:解:(1)由:(1)由

 =
= ,
,得a+1=-3,则a=-4(3分)
(2)由(1)知
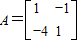 ,
,所以,由F(λ)=
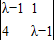 得:λ1=-1,λ2=3(7分)
得:λ1=-1,λ2=3(7分)λ1=-1时,由-2x+y=0得:y=-2x取
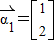
λ2=3时,由2x+y=0得:y=-2x,取
 .(9分)
.(9分)所以,A的特征值为-1或3.
属于-1的一个特征向量
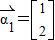 ,
,属于3的一个特征向量
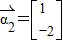 (10分)
(10分)点评:本题考查二阶矩阵,考查二阶矩阵的特征值的求法,考查二阶矩阵的特征向量的求法,因为是高等数学的内容,考查的比较简单,是一个中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
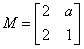 ,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0)。
,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P′(-4,0)。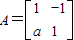 ,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3),
,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3),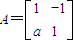 ,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3),
,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3),