题目内容
17.当a取何值时,求方程ax2-2x+1=0的一个根在(0,1)上,另一个根在(1,2)上.分析 构造函数f(x)=ax2-2x+1,利用根的存在性定理,列出不等式组$\left\{\begin{array}{l}{f(0)•f(1)<0}\\{f(1)•f(2)<0}\end{array}\right.$,求出解集即可.
解答 解:设f(x)=ax2-2x+1,
∵关于x的方程ax2-2x+1=0的一个根在(0,1)上,另一个根在(1,2)上,
∴$\left\{\begin{array}{l}{f(0)•f(1)<0}\\{f(1)•f(2)<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a-1<0}\\{(a-1)(4a-3)<0}\end{array}\right.$,
解得$\frac{3}{4}$<a<1;
∴a的取值范围是($\frac{3}{4}$,1).
点评 本题考查了方程的根与函数零点的应用问题,解题时应结合零点的存在定理,是基础题目.

练习册系列答案
相关题目
 终边上一点
终边上一点 ,则
,则 的值为________.
的值为________. 中,
中, 分别为角
分别为角 的对边,若
的对边,若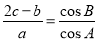 .
.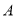 的大小;
的大小;  ,求
,求