��Ŀ����
13����֪����$\overrightarrow{a}$=��3��0����$\overrightarrow{b}$=��0��2����������$\overrightarrow{c}$���㣨$\overrightarrow{a}-\overrightarrow{c}$���ͣ�$\overrightarrow{c}-\overrightarrow{b}$������|$\overrightarrow{c}$|��ȡֵ��Χ������ �����⣬��$\overrightarrow{c}$=��x��y�����õ���$\overrightarrow{a}-\overrightarrow{c}$���ͣ�$\overrightarrow{c}-\overrightarrow{b}$�������꣬���ô�ֱ�����ʵõ�����x��y��ʽ������ģ�ķ�Χ��
��� �⣺��$\overrightarrow{c}$=��x��y����
��$\overrightarrow{a}-\overrightarrow{c}$=��3-x��-y����$\overrightarrow{c}-\overrightarrow{b}$=��x��y-2����
��Ϊ��$\overrightarrow{a}-\overrightarrow{c}$���ͣ�$\overrightarrow{c}-\overrightarrow{b}$����
���ԣ�$\overrightarrow{a}-\overrightarrow{c}$��•��$\overrightarrow{c}-\overrightarrow{b}$��=0������3-x��x-y��y-2��=0��
���ԣ�x-$\frac{3}{2}$��2+��y-1��2=$\frac{13}{4}$��
����|$\overrightarrow{c}$|=$\sqrt{{x}^{2}+{y}^{2}}$����ʾԲ�ϵĵ㵽ԭ��ľ��룬
�������ֵΪ$\frac{\sqrt{13}}{2}��2=\sqrt{13}$����СֵΪ0��
����|$\overrightarrow{c}$|��ȡֵ��ΧΪ[0��$\sqrt{13}$]��
���� ���⿼�����������������㡢������ֱ�������Լ�����������ģ�ļ���������ģ����ֵ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{\sqrt{3}}{2}$ |
 �Ķ�����Ϊ ��
�Ķ�����Ϊ �� ����
���� �ķ���
�ķ���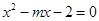 ��
�� �н⣬����
�н⣬���� ��
�� ������������
������������ Ϊ�����⣬
Ϊ�����⣬ �������⣬��ʵ��
�������⣬��ʵ�� ��ȡֵ��Χ��
��ȡֵ��Χ��