题目内容
【题目】已知函数![]() (
(![]() 是自然对数的底数)与
是自然对数的底数)与![]() 的图象上存在关于
的图象上存在关于![]() 轴对称的点,则实数
轴对称的点,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】根据题意,若函数f(x)=﹣x3+1+a(![]() ≤x≤e,e是自然对数的底)与g(x)=3lnx的图象上存在关于x轴对称的点,
≤x≤e,e是自然对数的底)与g(x)=3lnx的图象上存在关于x轴对称的点,
则方程﹣x3+1+a=﹣3lnx在区间[![]() ,e]上有解,
,e]上有解,
﹣x3+1+a=﹣3lnxa+1=x3﹣31nx,即方程a+1=x3﹣31nx在区间[![]() ,e]上有解,
,e]上有解,
设函数g(x)=x3﹣31nx,其导数g′(x)=3x2﹣![]() =
=![]() ,
,
又由x∈[![]() ,e],g′(x)=0在x=1有唯一的极值点,
,e],g′(x)=0在x=1有唯一的极值点,
分析可得:当![]() ≤x≤1时,g′(x)<0,g(x)为减函数,
≤x≤1时,g′(x)<0,g(x)为减函数,
当1≤x≤e时,g′(x)>0,g(x)为增函数,
故函数g(x)=x3﹣31nx有最小值g(1)=1,
又由g(![]() )=
)=![]() +3,g(e)=e3﹣3;比较可得:g(
+3,g(e)=e3﹣3;比较可得:g(![]() )<g(e),
)<g(e),
故函数g(x)=x3﹣31nx有最大值g(e)=e3﹣3,
故函数g(x)=x3﹣31nx在区间[![]() ,e]上的值域为[1,e3﹣3];
,e]上的值域为[1,e3﹣3];
若方程a+1=x3﹣31nx在区间[![]() ,e]上有解,
,e]上有解,
必有1≤a+1≤e3﹣3,则有0≤a≤e3﹣4,
即a的取值范围是[0,e3﹣4];

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送每张面额为
向用户随机派送每张面额为![]() 元,
元,元,
![]() 元的 三种骑行券.用户每次使用
元的 三种骑行券.用户每次使用![]() 扫码用车后,都可获得一张骑行券.用户骑行一次获得
扫码用车后,都可获得一张骑行券.用户骑行一次获得![]() 元券,获得
元券,获得![]() 元券的概率分别是
元券的概率分别是![]() ,
,![]() ,且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为
,且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
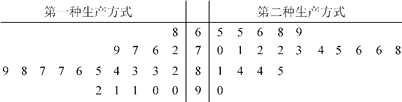
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
【题目】已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.