题目内容
已知函数f(x)的定义域为[0，1]，且满足下列条件：①对于任意x∈[0，1]，总有f(x)≥3且f(1)=4.②若x1≥0,x2≥0,x1+x2≤1.则有f(x1+x2)≥f(x1)+f(x3)-3.(1)求f(0)的值；
(2)求证:f(x)≤4；
(3)当x∈(
,
)(n=1,2,3…)时，试证明f(x)＜3x+3.
答案：(1)解：∵当x∈［0,1］时，f(x)≥3,
∴f(0)≥3,又在f(x1+x2)≥f(x1)+f(x2)-3中
令x1=x2=0,得f(0)≤3,∴f(0)=3.
(2)证明：设0≤x1＜x2≤1.∴0＜x2-x1≤1,
∴f(x2)-f(x1)=f［(x2-x1)+x1］-f(x1)≥f(x2-x1)+f(x1)-3-f(x1)=f(x2-x1)-3≥0,
若f(x2-x1)-3=0,即f(x2-x1)=3,则f(x)在[0，1]上恒为3，这与f(1)=4矛盾.
∴f(x2-x1)＞3,即f(x)在[0，1]上为单调递增函数,∴f(x)≤f(1)=4.
(3)证明：由f(x1+x2)≥f(x1)+f(x2)-3,令x1=x2=x,得f(x)≤.
取x=,得f(
)≤
≤
+3,x=
时,f(
)≤
.
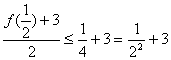由数学归纳法得f(
)≤
+3.∴取x∈(
)时，则有f(x)＜2x+2,
而x∈(
)
(
),∴f(x)＜2x+2.
而在(
)上2x+2＜3x+3,∴当x∈(
)时,f(x)＜3x+3成立.
练习册系列答案
相关题目