题目内容
设不等式|2x-1|<1的解集为M.
(1)求集合M;
(2)若a,b∈M,试比较ab+1与a+b的大小.
(1) M={x|0<x<1}.(2) ab+1>a+b.
解析试题分析:(1)由|2x-1|<1得-1<2x-1<1,解得0<x<1.
所以M={x|0<x<1}.
(2)由(1)和a,b∈M可知0<a<1,0<b<1.
所以(ab+1)-(a+b)=(a-1)(b-1)>0,
故ab+1>a+b.
考点:本题主要考查简单绝对值不等式的解法,比较大小的方法。
点评:简单题,比较大小的方法可采用“差比法”—“作差—变形---定号”。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
当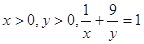 时,
时,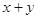 的最小值为( )
的最小值为( )
| A.10 | B.12 | C.14 | D.16 |
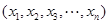 满足条件:
满足条件: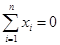 ; ②
; ②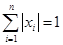 .
.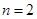 时,求
时,求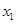 ,
,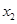 的值;
的值;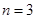 时,求证:
时,求证: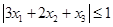 ;
;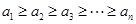 ,且
,且
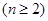 ,求证:
,求证: .
.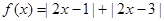 ,
,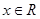 .
. ;
;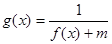 的定义域为
的定义域为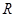 ,求实数
,求实数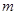 的取值范围.
的取值范围.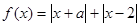
 的解集
的解集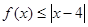 的解集包含[1,2],求
的解集包含[1,2],求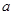 的取值范围
的取值范围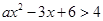 的解集为
的解集为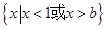 .
.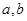 ;
;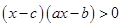 .
.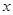 的不等式
的不等式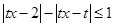 ,其中
,其中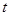 是实参数.
是实参数.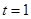 时,解上面的不等式.
时,解上面的不等式.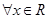 ,上面的不等式均成立,求实数
,上面的不等式均成立,求实数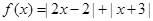 .
.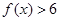 ;
; 的不等式
的不等式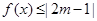 的解集不是空集,试求实数
的解集不是空集,试求实数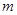 的取值范围.
的取值范围.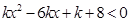 的解集为空集,求实数k的取值范围.
的解集为空集,求实数k的取值范围.