题目内容
用秦九韶算法计算 时的值时,需要运算 次
时的值时,需要运算 次
 时的值时,需要运算 次
时的值时,需要运算 次9
试题分析:求多项式的值时,首先计算最内层括号内一次多项式的值,即v1=anx+an-1然后由内向外逐层计算一次多项式的值,即v2=v1x+an-2,v3=v2x+an-3…,vn=vn-1x+a1,这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.解:f(x)=anxn+an-1xn-1+…+a1x+a0=(anxn-1+an-1xn-2+…+a1)x+a0,=((anxn-2+an-1xn-3+…+a2)x+a1)x+a0,=…,=(…((anx+an-1)x+an-2)x+…+a1)x+a0.,求多项式的值时,首先计算最内层括号内一次多项式的值,即,v1=anx+an-1,然后由内向外逐层计算一次多项式的值,即,v2=v1x+an-2 v3=v2x+an-3,…,vn=vn-1x+a1,这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.,∴对于一个n次多项式,至多做n次乘法和n次加法计算
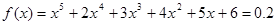 时的值时最高次为5次,那么可知需要运算9次,故答案为9.
时的值时最高次为5次,那么可知需要运算9次,故答案为9.点评:秦九韶算法对于一个n次多项式,至多做n次乘法和n次加法.

练习册系列答案
相关题目
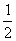 +
+ -
- +…+
+…+ 的程序框图,请将框图内所缺的式子填充,并写出程序.
的程序框图,请将框图内所缺的式子填充,并写出程序. 

 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据。
(吨标准煤)的几组对照数据。 ;
;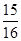 ,则输入的整数a为
,则输入的整数a为 。
。