题目内容
对于直线L:y=kx+1是否存在这样的实数,使得L与双曲线C:3x2-y2=1的交点A,B关于直线y=ax(a为常数)对称?若存在,求k的值;若不存在,说明理由.
分析:利用两点关于直线对称满足两点的中点在直线上;两点连线与对称轴垂直列出方程组,将韦达定理代入得到a,k关系.判断出是否存在.
解答:证明:(反证法)假设存在实数k,使得A、B关于直线y=ax对称,(1分)
设A( x1,y1),B( x2,y2),(2分)
则
,(6分)
由
得(3-k2)x2-2kx-2=0,(4)(8分)
由(2)(3)有a(x1+x2)=k(x1+x2)+2,(5)(9分)
由(4)知x1+x2=
,(10分)
代入(5)整理得ak=3,与(1)矛盾,(12分)
故不存在实数k,使得A、B关于直线y=ax对称,(14分)
设A( x1,y1),B( x2,y2),(2分)
则
|
由
|
由(2)(3)有a(x1+x2)=k(x1+x2)+2,(5)(9分)
由(4)知x1+x2=
| 2k |
| 3-k2 |
代入(5)整理得ak=3,与(1)矛盾,(12分)
故不存在实数k,使得A、B关于直线y=ax对称,(14分)
点评:本题考查解决直线与圆锥曲线的位置关系常将它们的方程联立,处理两点关于直线对称的问题常借用两点的中点在对称轴上;两点连线与对称轴垂直.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
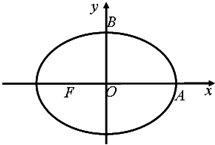 如图,点F是椭圆W:
如图,点F是椭圆W: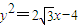 的顶点为双曲线的右焦点,抛物线的准线为双曲线的右准线.
的顶点为双曲线的右焦点,抛物线的准线为双曲线的右准线.