题目内容
设双曲线C的中心在原点,以抛物线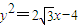 的顶点为双曲线的右焦点,抛物线的准线为双曲线的右准线.
的顶点为双曲线的右焦点,抛物线的准线为双曲线的右准线.(1)试求双曲线C的方程;
(2)设直线l:y=2x+1与双曲线C交于A、B两点,求|AB|;
(3)对于直线L:y=kx+1,是否存在这样的实数k,使直线L与双曲线C的交点A、B关于直线y=ax(a为常数)对称,若存在,求出k的值;若不存在,请说明理由.
【答案】分析:(1)由抛物线y2=2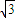 x-4,即y2=2
x-4,即y2=2 (x-
(x-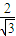 ),可知抛物线顶点为(
),可知抛物线顶点为(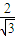 ,0),准线方程为x=
,0),准线方程为x=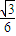 .在双曲线C中,中心在原点,右焦点(
.在双曲线C中,中心在原点,右焦点(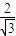 ,0),右准线x=
,0),右准线x=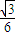 ,由此能求出双曲线C的方程.
,由此能求出双曲线C的方程.
(2)由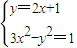 ,知3x2-(2x+1)2=1,由此能求出|AB|.
,知3x2-(2x+1)2=1,由此能求出|AB|.
(3)设存在实数k,使A、B关于直线y=ax对称,设A(x1,y1)、B(x2,y2),则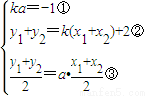 ,由此能够推导出不存在实数k,使A、B关于直线y=ax对称.
,由此能够推导出不存在实数k,使A、B关于直线y=ax对称.
解答:解:(1)由抛物线y2=2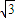 x-4,即y2=2
x-4,即y2=2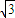 (x-
(x-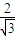 ),可知抛物线顶点为(
),可知抛物线顶点为(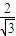 ,0),准线方程为x=
,0),准线方程为x=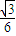 .
.
在双曲线C中,中心在原点,右焦点(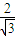 ,0),
,0),
右准线x=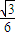 ,∴
,∴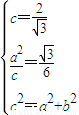 ⇒
⇒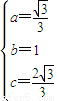
∴双曲线C的方程3x2-y2=1
(2)由 ⇒3x2-(2x+1)2=1⇒x2+4x+2=0∴|AB|=2
⇒3x2-(2x+1)2=1⇒x2+4x+2=0∴|AB|=2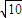
(3)假设存在实数k,使A、B关于直线y=ax对称,设A(x1,y1)、B(x2,y2),则
 由
由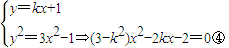
由②③,有a(x1+x2)=k(x1+x2)+2 ⑤
由④知:x1+x2=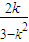 代入⑤
代入⑤
整理得ak=3与①矛盾,故不存在实数k,使A、B关于直线y=ax对称.
点评:本题考查双曲线方程的求法、求弦长和判断是否存在存在满足条件的实数k.解题时要认真审题,注意合理地进行等价转化.
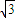 x-4,即y2=2
x-4,即y2=2 (x-
(x-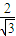 ),可知抛物线顶点为(
),可知抛物线顶点为(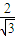 ,0),准线方程为x=
,0),准线方程为x=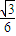 .在双曲线C中,中心在原点,右焦点(
.在双曲线C中,中心在原点,右焦点(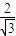 ,0),右准线x=
,0),右准线x=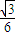 ,由此能求出双曲线C的方程.
,由此能求出双曲线C的方程.(2)由
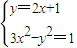 ,知3x2-(2x+1)2=1,由此能求出|AB|.
,知3x2-(2x+1)2=1,由此能求出|AB|.(3)设存在实数k,使A、B关于直线y=ax对称,设A(x1,y1)、B(x2,y2),则
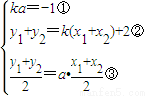 ,由此能够推导出不存在实数k,使A、B关于直线y=ax对称.
,由此能够推导出不存在实数k,使A、B关于直线y=ax对称.解答:解:(1)由抛物线y2=2
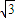 x-4,即y2=2
x-4,即y2=2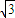 (x-
(x-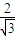 ),可知抛物线顶点为(
),可知抛物线顶点为(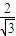 ,0),准线方程为x=
,0),准线方程为x=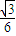 .
.在双曲线C中,中心在原点,右焦点(
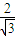 ,0),
,0),右准线x=
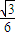 ,∴
,∴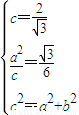 ⇒
⇒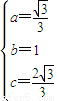
∴双曲线C的方程3x2-y2=1
(2)由
 ⇒3x2-(2x+1)2=1⇒x2+4x+2=0∴|AB|=2
⇒3x2-(2x+1)2=1⇒x2+4x+2=0∴|AB|=2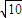
(3)假设存在实数k,使A、B关于直线y=ax对称,设A(x1,y1)、B(x2,y2),则
 由
由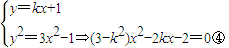
由②③,有a(x1+x2)=k(x1+x2)+2 ⑤
由④知:x1+x2=
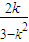 代入⑤
代入⑤整理得ak=3与①矛盾,故不存在实数k,使A、B关于直线y=ax对称.
点评:本题考查双曲线方程的求法、求弦长和判断是否存在存在满足条件的实数k.解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
相关题目
 的焦点,且该点到双曲线的一条准线的距离为
的焦点,且该点到双曲线的一条准线的距离为 .
. 的焦点,且该点到双曲线的一条准线的距离为
的焦点,且该点到双曲线的一条准线的距离为 .
.