题目内容
若对于任意的x∈[a,b],函数f(x),g(x)总满足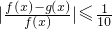 ,则称在区间[a,b]上,g(x)可以代替f(x).若
,则称在区间[a,b]上,g(x)可以代替f(x).若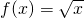 ,则下列函数中,可以在区间[4,16]上代替f(x)的是
,则下列函数中,可以在区间[4,16]上代替f(x)的是
- A.g(x)=x-2
- B.
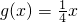
- C.
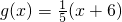
- D.g(x)=2x-6
C
分析:根据已知中对于任意的x∈[a,b],函数f(x),g(x)总满足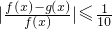 ,则称在区间[a,b]上,g(x)可以代替f(x).若
,则称在区间[a,b]上,g(x)可以代替f(x).若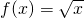 ,我们分别求出四个答案中的g(x)的解析式,对应的
,我们分别求出四个答案中的g(x)的解析式,对应的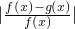 在区间[4,16]上的值域,判断与
在区间[4,16]上的值域,判断与 的关键后,即可得到答案.
的关键后,即可得到答案.
解答:∵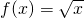 ,
,
∴在区间[4,16]上,
当g(x)=x-2时,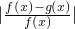 =|1-(
=|1-( )|∈[0,
)|∈[0, ],不满足要求;
],不满足要求;
当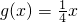 时,
时,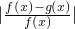 =|1-
=|1- |∈[0,
|∈[0, ],不满足要求;
],不满足要求;
当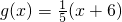 时,
时,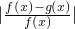 =|1-(
=|1-(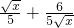 )|∈[0,
)|∈[0, ]满足要求;
]满足要求;
当g(x)=2x-6时,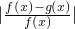 =|1-(2
=|1-(2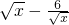 )|∈[0,
)|∈[0,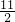 ],不满足要求;
],不满足要求;
故选C
点评:本题考查的知识点是函数的值域,其中根据函数的单调性及基本不等式求出四个答案对应的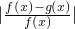 在区间[4,16]上的值域,是解答本题的关键.
在区间[4,16]上的值域,是解答本题的关键.
分析:根据已知中对于任意的x∈[a,b],函数f(x),g(x)总满足
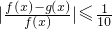 ,则称在区间[a,b]上,g(x)可以代替f(x).若
,则称在区间[a,b]上,g(x)可以代替f(x).若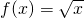 ,我们分别求出四个答案中的g(x)的解析式,对应的
,我们分别求出四个答案中的g(x)的解析式,对应的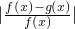 在区间[4,16]上的值域,判断与
在区间[4,16]上的值域,判断与 的关键后,即可得到答案.
的关键后,即可得到答案.解答:∵
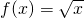 ,
,∴在区间[4,16]上,
当g(x)=x-2时,
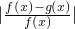 =|1-(
=|1-( )|∈[0,
)|∈[0, ],不满足要求;
],不满足要求;当
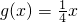 时,
时,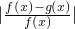 =|1-
=|1- |∈[0,
|∈[0, ],不满足要求;
],不满足要求;当
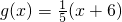 时,
时,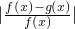 =|1-(
=|1-(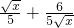 )|∈[0,
)|∈[0, ]满足要求;
]满足要求;当g(x)=2x-6时,
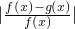 =|1-(2
=|1-(2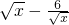 )|∈[0,
)|∈[0,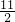 ],不满足要求;
],不满足要求;故选C
点评:本题考查的知识点是函数的值域,其中根据函数的单调性及基本不等式求出四个答案对应的
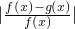 在区间[4,16]上的值域,是解答本题的关键.
在区间[4,16]上的值域,是解答本题的关键. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设a>1,若对于任意的x∈[a,2a],都有y∈[a,a2]满足方程logax+logay=3,这时a的取值集合为( )
| A、{a|1<a≤2} | B、{a|a≥2} | C、{a|2≤a≤3} | D、{2,3} |
若对于任意的x∈[a,b],函数f(x),g(x)总满足|
|≤
,则称在区间[a,b]上,g(x)可以代替f(x).若f(x)=
,则下列函数中,可以在区间[4,16]上代替f(x)的是( )
| f(x)-g(x) |
| f(x) |
| 1 |
| 10 |
| x |
| A、g(x)=x-2 | ||
B、g(x)=
| ||
C、g(x)=
| ||
| D、g(x)=2x-6 |