题目内容
(本小题满分16分)
已知数列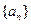 满足
满足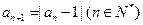 ,(1)若
,(1)若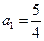 ,求
,求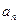 ;
;
(2)是否存在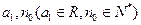 ,使当
,使当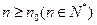 时,
时,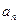 恒为常数。若存在求
恒为常数。若存在求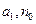 ,否则说明理由;
,否则说明理由;
(3)若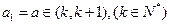 ,求
,求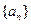 的前
的前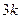 项的和
项的和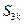 (用
(用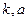 表示)
表示)
已知数列
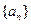 满足
满足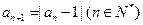 ,(1)若
,(1)若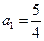 ,求
,求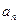 ;
;(2)是否存在
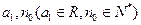 ,使当
,使当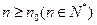 时,
时,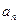 恒为常数。若存在求
恒为常数。若存在求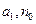 ,否则说明理由;
,否则说明理由;(3)若
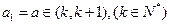 ,求
,求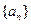 的前
的前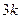 项的和
项的和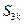 (用
(用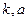 表示)
表示)解: (1)设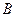
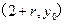 ,过圆心
,过圆心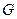 作
作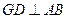 于
于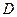 ,
,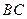 交长轴于
交长轴于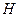
由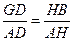 得
得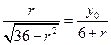 ,即
,即 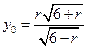 (1)
(1)
而点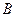
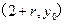
 在椭圆上,
在椭圆上,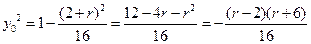 (2)
(2)
由(1)、 (2)式得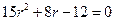 ,解得
,解得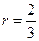 或
或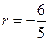 (舍去)
(舍去)
(2) 设过点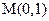 与圆
与圆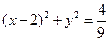 相切的直线方程为:
相切的直线方程为: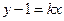 (3)
(3)
则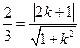 ,即
,即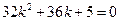 (4)
(4)
解得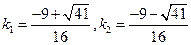
将(3)代入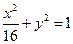 得
得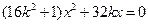 ,则异于零的解为
,则异于零的解为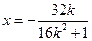
设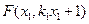 ,
,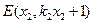 ,则
,则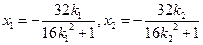
则直线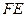 的斜率为:
的斜率为: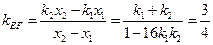
于是直线 的方程为:
的方程为: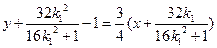 即
即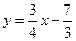
则圆心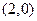 到直线
到直线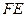 的距离
的距离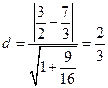 故结论成立.
故结论成立.
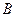
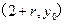 ,过圆心
,过圆心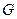 作
作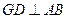 于
于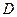 ,
,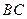 交长轴于
交长轴于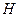
由
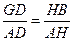 得
得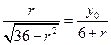 ,即
,即 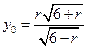 (1)
(1) 而点
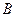
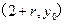
 在椭圆上,
在椭圆上,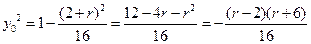 (2)
(2)由(1)、 (2)式得
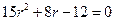 ,解得
,解得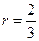 或
或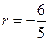 (舍去)
(舍去)(2) 设过点
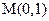 与圆
与圆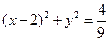 相切的直线方程为:
相切的直线方程为: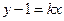 (3)
(3)则
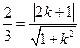 ,即
,即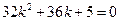 (4)
(4)解得
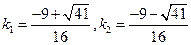
将(3)代入
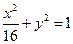 得
得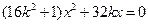 ,则异于零的解为
,则异于零的解为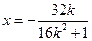
设
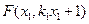 ,
,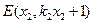 ,则
,则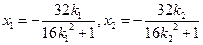
则直线
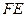 的斜率为:
的斜率为: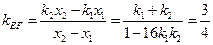
于是直线
 的方程为:
的方程为: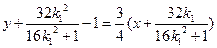 即
即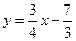
则圆心
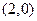 到直线
到直线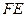 的距离
的距离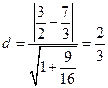 故结论成立.
故结论成立.略

练习册系列答案
相关题目
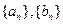 满足
满足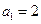 ,
,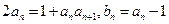 ,设数列
,设数列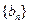 的前n项和为
的前n项和为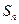 ,令
,令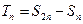 。
。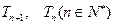 的大小,并说明理由。
的大小,并说明理由。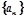 是公差不为0的等差数列,
是公差不为0的等差数列,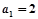 且
且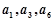 成等比数列,则
成等比数列,则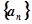 的前
的前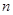 项和
项和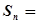
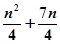
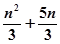
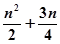
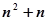
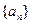 满足:
满足: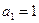 ,
,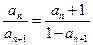
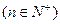 ,
,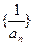 是等差数列;求
是等差数列;求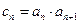
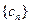 的前
的前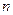 项和
项和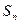 。
。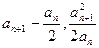 )为直线y=x的方向向量,a
)为直线y=x的方向向量,a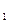 =1,则数列
=1,则数列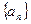 的前2011项的和为_______.
的前2011项的和为_______.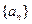 的前n项和为
的前n项和为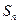 ,且2
,且2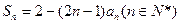
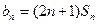 ,求数列
,求数列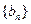 的通项公式;
的通项公式;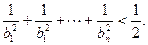
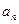 }中,
}中,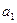 =
=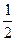 ,
,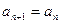 +
+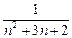 (n
(n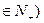 ,则
,则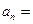 ( )
( )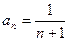
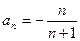
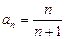
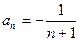
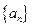 中,
中,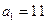 ,且
,且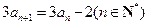 ,则该数列中相邻两项乘积的最小值为__________.
,则该数列中相邻两项乘积的最小值为__________.