题目内容
关于x的不等式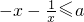 在区间[1,2]上有解,求a的取值范围.
在区间[1,2]上有解,求a的取值范围.
解:设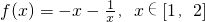 ,则
,则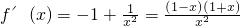 ,
,
所以x∈[1,2]时,f'(x)≤0,即f(x)在区间[1,2]上是减函数,
所以,x∈[1,2]时,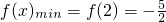 .
.
因为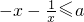 在区间[1,2]上有解,所以
在区间[1,2]上有解,所以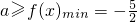
故a的取值范围是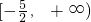 .
.
分析:设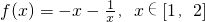 ,不等式
,不等式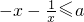 在区间[1,2]上有解,等价于a≥f(x)min,利用导数求得函数的最小值,即可求得a的取值范围.
在区间[1,2]上有解,等价于a≥f(x)min,利用导数求得函数的最小值,即可求得a的取值范围.
点评:本题考查不等式有解,考查利用导数求函数的最值,解题的关键是求函数的最小值.
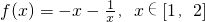 ,则
,则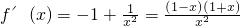 ,
,所以x∈[1,2]时,f'(x)≤0,即f(x)在区间[1,2]上是减函数,
所以,x∈[1,2]时,
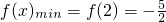 .
.因为
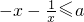 在区间[1,2]上有解,所以
在区间[1,2]上有解,所以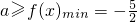
故a的取值范围是
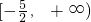 .
.分析:设
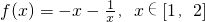 ,不等式
,不等式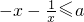 在区间[1,2]上有解,等价于a≥f(x)min,利用导数求得函数的最小值,即可求得a的取值范围.
在区间[1,2]上有解,等价于a≥f(x)min,利用导数求得函数的最小值,即可求得a的取值范围.点评:本题考查不等式有解,考查利用导数求函数的最值,解题的关键是求函数的最小值.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
 在区间
在区间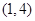 内有解,则实数a的取值范围是( )
内有解,则实数a的取值范围是( )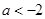 B.
B.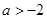 C.
C.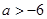 D.
D.
 在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围; 都成立.
都成立.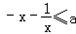 在区间[1,2]上有解,求a的取值范围.
在区间[1,2]上有解,求a的取值范围.