题目内容
(1)己知z=x+yi(x,y∈R)满足|z-4i|-|z+2|=0,求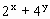 的最小值.
的最小值.
(2)设复数z满足2|z-3-3i|-|z|=0,试求|z|的最大值和最小值.
答案:
解析:
提示:
解析:
|
解:(1)由已知条件得 (2)解法1:设z=x+yi(x,y∈R),得2|x+yi-3-3i|-|x+yi|=0, 解法2:设z=r(cosθ+isinθ),代入已知条件并化简得 解法3:将解法1中的方程 解法4:由已知得|z-(3+3i)|= |
提示:
|
注 本题的四种解法从不同的侧面反映了求复数模的极值的常用方法:不等式法、三角法、几何法、公式法,它们的共同之处是把复数问题化归为实数问题来解. |

练习册系列答案
相关题目
 ,即x+2y=3,∴
,即x+2y=3,∴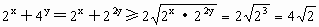 ,即得
,即得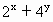 的最小值为
的最小值为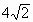 .
. =0,化简得
=0,化简得 -8(x+y)+24=0.∵x+y≤
-8(x+y)+24=0.∵x+y≤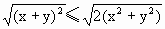 ,故得
,故得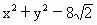
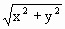 +24≤0,即
+24≤0,即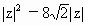 +24≤0.解得
+24≤0.解得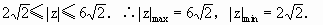
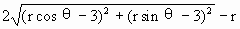 =0,化简得
=0,化简得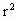 -8r(cosθ+sinθ)+24=0,
-8r(cosθ+sinθ)+24=0, +24=0.∴
+24=0.∴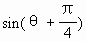 ≤1,∴
≤1,∴
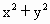 -8(x+y)+24=0,化为
-8(x+y)+24=0,化为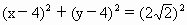 .可知它表示以点(4,4)为圆心,
.可知它表示以点(4,4)为圆心,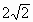 为半径的圆,∴|z|的最大值和最小值分别是圆上的点到坐标原点距离的最大值和最小值.∴
为半径的圆,∴|z|的最大值和最小值分别是圆上的点到坐标原点距离的最大值和最小值.∴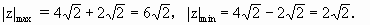
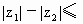
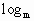 x+(c-a)
x+(c-a)