题目内容

如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ
(0<θ<).
(1)求证:平面VAB⊥平面VCD;
(2)当角θ变化时,求直线BC与平面VAB所成的角的取值范围.
分析:解法一(几何法)(1)由已知中AC=BC,D是AB的中点,由等腰三角形三线合一,可得CD⊥AB,又由VC⊥底面ABC,由线面垂直的性质可得VC⊥AB,结合线面垂直的判定定理可得AB⊥平面VCD,再由面面垂直的判定定理可得平面VAB⊥平面VCD;
(2)过点C在平面VCD内作CH⊥VD于H,连接BH,可得∠CBH就是直线BC与平面VAB所成的角,设∠CBH=φ,根据
CH=asinθ=asinφ,易得到直线BC与平面VAB所成角的取值范围.
解法二(向量法)(1)以CA,CB,CV所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,分析求出
,
,
易得根据向量数量积为0,得到CD⊥AB,VC⊥AB,结合线面垂直的判定定理可得AB⊥平面VCD,再由面面垂直的判定定理可得平面VAB⊥平面VCD;
(2)令直线BC与平面VAB所成的角为φ,求出平面VAB的一个法向量和
,由向量夹角公式,易得到
sin?=||=sinθ,进而得到直线BC与平面VAB所成角的取值范围.
解答: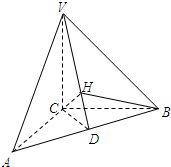
解:法一(几何法):
证明:(1)∵AC=BC=a
∴△ACB是等腰三角形,
又D是AB的中点∴CD⊥AB,
又VC⊥底面ABC∴VC⊥AB
于是AB⊥平面VCD.
又AB?平面VAB∴平面VAB⊥平面VCD
解:(2)过点C在平面VCD内作CH⊥VD于H,连接BH
则由(1)知AB⊥CH,∴CH⊥平面VAB
于是∠CBH就是直线BC与平面VAB所成的角.
在Rt△CHD中,CD=
a,
CH=asinθ;
设∠CBH=φ,在Rt△BHC中,CH=asinφ∴
sinθ=sinφ∵
0<θ<∴0<sinθ<1,
0<sinφ<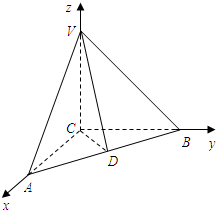
又
0≤φ≤,∴
0<φ<即直线BC与平面VAB所成角的取值范围为
(0,).
法二(向量法):
证明:(1)以CA,CB,CV所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则
C(0,0,0),A(a,0,0),B(0,a,0),D(,,0),V(0,0,atanθ),
于是,
=(,,-atanθ),
=(,,0),
=(-a,a,0).
从而
•=(-a,a,0)•(,,0)=-a2+a2+0=0,即AB⊥CD.
同理
•=(-a,a,0)•(,,-atanθ)=-a2+a2+0=0,
即AB⊥VD.又CD∩VD=D,∴AB⊥平面VCD.
又AB?平面VAB.∴平面VAB⊥平面VCD.
解:(2)设直线BC与平面VAB所成的角为φ,平面VAB的一个法向量为n=(x,y,z),
则由
n•=0,n•=0.
得
可取
n=(1,1,cotθ),又
=(0,-a,0),
于是
sinφ=||==sinθ,
∵
0<θ<,∴0<sinθ<1,
0<sinφ<.
又
0≤φ≤,∴
0<φ<.
即直线BC与平面VAB所成角的取值范围为
(0,).
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面所成的角,其中方法一(几何法)的关键是熟练掌握线线垂直、线面垂直、面面垂直之间的转化,方法二(向量法)的关键是建立空间坐标系,将空间线线关系、线面夹角转化为向量夹角问题是解答本题的关键.
 一题一题找答案解析太慢了
一题一题找答案解析太慢了
下载作业精灵直接查看整书答案解析立即下载
练习册系列答案
相关题目
 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ< 解:法一(几何法):
解:法一(几何法):
 解:法一(几何法):
解:法一(几何法):

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ< 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.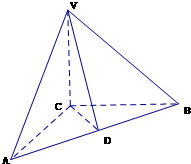 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°. .
.