题目内容
某糖果厂生产A、B两种糖果,A种糖果每箱可获利润40元,B种糖果每箱可获利润50元.其生产过程分混合、烹调、包装三道工序.下表为每箱糖果生产过程中所需平均时间(单位:min).| 混合 | 烹调 | 包装 | |
| A | 1 | 5 | 3 |
| B | 2 | 4 | 1 |
【答案】分析:先设生产A种糖果x箱,生产B种糖果y箱,可获利润z元,列出约束条件,再根据约束条件画出可行域,设z=40x+50y,再利用z的几何意义求最值,只需求出直线z=40x+50y过可行域内的点时,从而得到z值即可.
解答: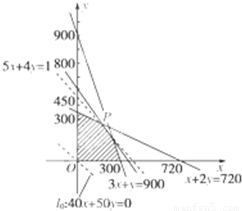 解:设生产A种糖果x箱,生产B种糖果y箱,可获利润z元,即求
解:设生产A种糖果x箱,生产B种糖果y箱,可获利润z元,即求
z=40x+50y在约束条件 下的最大值.
下的最大值.
作出可行域,如图.
作直线l:40x+50y=0,平移l经过点P时,
z=40x+50y取最大值,
解方程组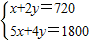 得P(120,300).
得P(120,300).
∴zmax=40×120+50×300=19 800.
所以生产A种糖果120箱,生产B种糖果300箱时,可以获得最大利润19 800元.
点评:在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件⇒②由约束条件画出可行域⇒③分析目标函数Z与直线截距之间的关系⇒④使用平移直线法求出最优解⇒⑤还原到现实问题中.
解答:
 解:设生产A种糖果x箱,生产B种糖果y箱,可获利润z元,即求
解:设生产A种糖果x箱,生产B种糖果y箱,可获利润z元,即求z=40x+50y在约束条件
 下的最大值.
下的最大值.作出可行域,如图.
作直线l:40x+50y=0,平移l经过点P时,
z=40x+50y取最大值,
解方程组
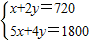 得P(120,300).
得P(120,300).∴zmax=40×120+50×300=19 800.
所以生产A种糖果120箱,生产B种糖果300箱时,可以获得最大利润19 800元.
点评:在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件⇒②由约束条件画出可行域⇒③分析目标函数Z与直线截距之间的关系⇒④使用平移直线法求出最优解⇒⑤还原到现实问题中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某糖果厂生产A、B两种糖果,A种糖果每箱可获利润40元,B种糖果每箱可获利润50元.其生产过程分混合、烹调、包装三道工序.下表为每箱糖果生产过程中所需平均时间(单位:min).
|
|
混合 |
烹调 |
包装 |
|
A |
1 |
5 |
3 |
|
B |
2 |
4 |
1 |
每种糖果的生产过程中,混合的设备至多用机器12 h,烹调的设备最多只能用机器30 h,包装的设备最多只能用机器15 h,每种糖果各生产多少箱可获得最大利润?
