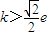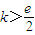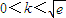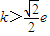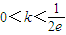Question

已知k＞0，函数f（x）=kx²-lnx在其定义域上有两个零点，则实数k的取值范围是（　　）

• A、k＞

  e

  2

• B、0＜k＜

  e

• C、k＞

  2

  2

  e
• D、0＜k＜

  1

  2e

Answer 1

分析：设函数g（x）=kx²与函数u（x）=lnx的图象相切时，k=k₁，则当0＜k＜k₁时，函数f（x）=kx²-lnx在其定义域上有两个零点．

解答：解：设g（x）=kx²与函数u（x）=lnx的图象相切
设（m，n）为两个函数图象的公切点
∵g'（x）=2kx，u'（x）=

1

x

则g'（m）=2km=u'（m）=

1

m

则m=

1 2k

此时n=ln

1 2k

即ln

1 2k

=k•

1

2k

=

1

2

解得：k=

1

2e

故函数f（x）=kx²-lnx在其定义域上有两个零点，则实数k的取值范围是0＜k＜

1

2e

故选D

点评：函数F（x）=f（x）-g（x）有两个零点，即函数f（x）的图象与函数g（x）的图形有两个交点，我们关键问题是找到两个函数的图象相切（即只有一个交点）时参数的值，即确定参数取值范围的端点．