题目内容
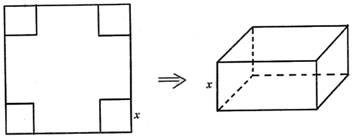
把边长为60cm的正方形铁皮的四角切去边长为xcm的相等的正方形,然后折成一个高度为xcm的无盖的长方体的盒子,要求长方体的高度与底面边长的比值不超过常数k(k>0),
(1)用x和k表示出长方体的体积的表达式V=V(x),并给出函数的定义域;
(2)问x取何值时,盒子的容积最大,最大容积是多少?
解:(1)设长方体高为xcm,则底面边长为(60-2x)cm,(0<x<30),
所以长方体容积V=V(x)=x(60-2x)2=4x(x-30)2;…(4分)
∵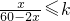 ,∴
,∴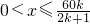 .
.
即函数定义域为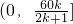 ,…(6分)
,…(6分)
(2)V′(x)=4(x-30)2+8x(x-30)=4(x-30)(3x-30)=12(x-30)(x-10)
令V′(x)=0,解得x=10,x=30(不合题意舍去)于是 …(8分)
①当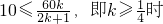 ,在x=10时,V取得最大值为Vmax=40•202=16000; …(10分)
,在x=10时,V取得最大值为Vmax=40•202=16000; …(10分)
②当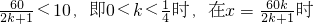 ,V取得最大值
,V取得最大值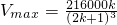 .…(12分)
.…(12分)
分析:(1)设长方体高为xcm,则底面边长为(60-2x)cm,(0<x<30),从而可得长方体容积的函数表达式,利用长方体的高度与底面边长的比值不超过常数k(k>0),可求函数定义域;
(2)对(1)中的函数表达式求导,确定函数的极值点,结合函数的定义域,分类求出V的最大值.
点评:本题以实际问题为载体,考查函数模型的关键,考查函数的最值,解题的关键是利用长方体的条件公式求出函数表达式,利用导数的方法求函数的最值,注意分类讨论.
所以长方体容积V=V(x)=x(60-2x)2=4x(x-30)2;…(4分)
∵
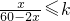 ,∴
,∴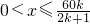 .
.即函数定义域为
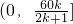 ,…(6分)
,…(6分)(2)V′(x)=4(x-30)2+8x(x-30)=4(x-30)(3x-30)=12(x-30)(x-10)
令V′(x)=0,解得x=10,x=30(不合题意舍去)于是 …(8分)
| x | (0,10) | 10 | (10,30) |
| V'(x) | + | 0 | - |
| V(x) | ↑ | ↓ |
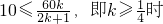 ,在x=10时,V取得最大值为Vmax=40•202=16000; …(10分)
,在x=10时,V取得最大值为Vmax=40•202=16000; …(10分)②当
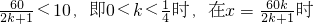 ,V取得最大值
,V取得最大值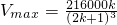 .…(12分)
.…(12分)分析:(1)设长方体高为xcm,则底面边长为(60-2x)cm,(0<x<30),从而可得长方体容积的函数表达式,利用长方体的高度与底面边长的比值不超过常数k(k>0),可求函数定义域;
(2)对(1)中的函数表达式求导,确定函数的极值点,结合函数的定义域,分类求出V的最大值.
点评:本题以实际问题为载体,考查函数模型的关键,考查函数的最值,解题的关键是利用长方体的条件公式求出函数表达式,利用导数的方法求函数的最值,注意分类讨论.

练习册系列答案
相关题目