题目内容
已知复数z1=3-4i,z2=1+i则复数| z12 | z2 |
分析:先利用两个复数代数形式的乘除法化简此复数到最简形式,求出此复数在复平面内对应点的坐标.
解答:解:∵复数z1=3-4i,z2=1+i,
∴
=
=
=
=-
,
此复数对应的点坐标为(-
,-
),在第三象限,
故答案为:三.
∴
| z12 |
| z2 |
| -7-24i |
| 1+i |
| (-7-24i)(1-i) |
| (1+i)(1-i) |
| -31-17i |
| 2 |
| 31+17i |
| 2 |
此复数对应的点坐标为(-
| 31 |
| 2 |
| 17 |
| 2 |
故答案为:三.
点评:本题考查两个复数代数形式的乘除法,复数与复平面内对应点间的关系,两个复数相除,分子和分母同时除以分母的共轭复数.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
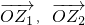 (其中O为坐标原点),记向量
(其中O为坐标原点),记向量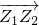 所对应的复数为z,则z的共轭复数为________.
所对应的复数为z,则z的共轭复数为________.