题目内容
已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
①求甲射击一次,命中不足8环的概率.
②求甲射击一次,至少命中7环的概率.
(1)甲射击一次,命中不足8环的概率是0.22.
(2)甲射击一次,至少命中7环的概率为0.9.
解析试题分析:记“甲射击一次,命中7环以下”为事件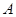 ,“甲射击一次,命中7环”为事件
,“甲射击一次,命中7环”为事件 ,由于在一次射击中,
,由于在一次射击中,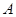 与
与 不可能同时发生,故
不可能同时发生,故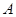 与
与 是互斥事件,
是互斥事件,
(1)“甲射击一次,命中不足8环”的事件为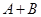 ,
,
由互斥事件的概率加法公式, .
.
答:甲射击一次,命中不足8环的概率是0.22.
(2)方法1:记“甲射击一次,命中8环”为事件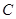 ,“甲射击一次,命中9环(含9环)以上”为事件
,“甲射击一次,命中9环(含9环)以上”为事件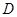 ,则“甲射击一次,至少命中7环”的事件为
,则“甲射击一次,至少命中7环”的事件为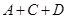 ,
,
∴ .
.
答:甲射击一次,至少命中7环的概率为0.9.
方法2:∵“甲射击一次,至少命中7环”为事件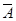 ,
,
∴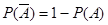 =1-0.1=0.9.
=1-0.1=0.9.
答:甲射击一次,至少命中7环的概率为0.9.
考点:本题主要考查互斥事件、对立事件的概念及其概率计算。
点评:中档题,本题解法较多。(2)解法二利用了对立事件概率公式,较为简洁。

为了保养汽车,维护汽车性能,汽车保养一般都在购车的4S店进行,某地大众汽车4S店售后服务部设有一个服务窗口专门接待保养预约。假设车主预约保养登记所需的时间互相独立,且都是整数分钟,对以往车主预约登记所需的时间统计结果如下:
| 登记所需时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(l)估计第三个车主恰好等待4分钟开始登记的概率:
(2)X表示至第2分钟末已登记完的车主人数,求X的分布列及数学期望.
为了参加 贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出
贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
| 班级 | 高三( )班 )班 | 高三( )班 )班 | 高二( )班 )班 | 高二( )班 )班 |
| 人数 | 12 | 6 | 9 | 9 |
(Ⅱ)该中学篮球队奋力拼搏,获得冠军.若要从高三年级抽出的队员中选出两位队员作为冠军的代表发言,求选出的两名队员来自同一班的概率.
(本小题满分12分)
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为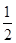 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
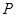 | 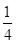 |  | 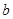 | 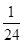 |
(2) 求
 ,
, 的值;
的值;(3) 求
 的数学期望.
的数学期望.  道备选题中一次性随机抽取
道备选题中一次性随机抽取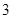 道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中
道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中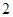 道题的便可通过.已知
道题的便可通过.已知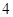 道题能正确完成,
道题能正确完成, ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.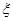 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和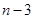 个白球.已知从
个白球.已知从 ,且
,且 。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于
。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于 。
。 为第一次取到白球时的取球次数,求
为第一次取到白球时的取球次数,求 。
。