题目内容
已知等差数列数﹛an﹜的前n项和为Sn,等比数列﹛bn﹜的各项均为正数,公比是q,且满足:a1=3,b1=1,b2+S2=12,S2=b2q.(Ⅰ)求an与bn;
(Ⅱ)设
 (λ∈R),若﹛cn﹜满足:cn+1>cn对任意的n∈N°恒成立,求λ的取值范围.
(λ∈R),若﹛cn﹜满足:cn+1>cn对任意的n∈N°恒成立,求λ的取值范围.
【答案】分析:(Ⅰ)由题目给出的已知条件b2+S2=12,S2=b2q,列关于等差数列的第二项及等比数列的公比的二元方程组,求出等差数列的第二项及等比数列的公比,则an与bn可求;
(Ⅱ)把(Ⅰ)中求得的an与bn代入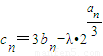 (λ∈R),整理后把cn+1>cn转化为含有λ和n的表达式,分离参数后利用函数的单调性求函数的最小值,从而求出λ的取值范围.
(λ∈R),整理后把cn+1>cn转化为含有λ和n的表达式,分离参数后利用函数的单调性求函数的最小值,从而求出λ的取值范围.
解答:解:(Ⅰ)由S2=a1+a2=3+a2,b2=b1q=q,且b2+S2=12,S2=b2q.
∴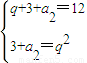 ,消去a2得:q2+q-12=0,解得q=3或q=-4(舍),
,消去a2得:q2+q-12=0,解得q=3或q=-4(舍),
∴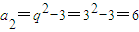 ,则d=a2-a1=6-3=3,
,则d=a2-a1=6-3=3,
从而an=a1+(n-1)d=3+3(n-1)=3n,
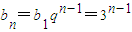 ;
;
(Ⅱ)∵an=3n,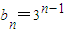 ,∴
,∴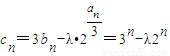 .
.
∵cn+1>cn对任意的n∈N*恒成立,即:3n+1-λ•3n+1>3n-λ•2n恒成立,
整理得:λ•2n<2•3n对任意的n∈N*恒成立,
即: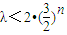 对任意的n∈N*恒成立.
对任意的n∈N*恒成立.
∵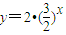 在区间[1,+∞)上单调递增,∴
在区间[1,+∞)上单调递增,∴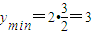 ,
,
∴λ<3.
∴λ的取值范围为(-∞,3).
点评:本题考查了等差数列与等比数列的通项公式,考查了利用分离变量法求参数的范围问题,借助于函数单调性求函数的最小值是解答此题的关键,此题是中档题.
(Ⅱ)把(Ⅰ)中求得的an与bn代入
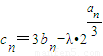 (λ∈R),整理后把cn+1>cn转化为含有λ和n的表达式,分离参数后利用函数的单调性求函数的最小值,从而求出λ的取值范围.
(λ∈R),整理后把cn+1>cn转化为含有λ和n的表达式,分离参数后利用函数的单调性求函数的最小值,从而求出λ的取值范围.解答:解:(Ⅰ)由S2=a1+a2=3+a2,b2=b1q=q,且b2+S2=12,S2=b2q.
∴
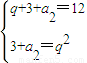 ,消去a2得:q2+q-12=0,解得q=3或q=-4(舍),
,消去a2得:q2+q-12=0,解得q=3或q=-4(舍),∴
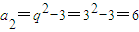 ,则d=a2-a1=6-3=3,
,则d=a2-a1=6-3=3,从而an=a1+(n-1)d=3+3(n-1)=3n,
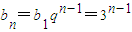 ;
;(Ⅱ)∵an=3n,
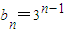 ,∴
,∴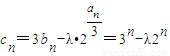 .
.∵cn+1>cn对任意的n∈N*恒成立,即:3n+1-λ•3n+1>3n-λ•2n恒成立,
整理得:λ•2n<2•3n对任意的n∈N*恒成立,
即:
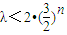 对任意的n∈N*恒成立.
对任意的n∈N*恒成立.∵
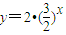 在区间[1,+∞)上单调递增,∴
在区间[1,+∞)上单调递增,∴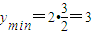 ,
,∴λ<3.
∴λ的取值范围为(-∞,3).
点评:本题考查了等差数列与等比数列的通项公式,考查了利用分离变量法求参数的范围问题,借助于函数单调性求函数的最小值是解答此题的关键,此题是中档题.

练习册系列答案
相关题目
 (λ∈R),若﹛cn﹜满足:cn+1>cn对任意的n∈N+恒成立,求λ的取值范围.
(λ∈R),若﹛cn﹜满足:cn+1>cn对任意的n∈N+恒成立,求λ的取值范围. (λ∈R),若﹛cn﹜满足:cn+1>cn对任意的n∈N°恒成立,求λ的取值范围.
(λ∈R),若﹛cn﹜满足:cn+1>cn对任意的n∈N°恒成立,求λ的取值范围.