题目内容
定义域为R的函数f(x)满足f(x+2)=3f(x),当x∈[0,2]时,f(x)=x2-2x,若x∈[-4,-2]时,f(x)≥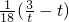 恒成立,则实数t的取值范围是________.
恒成立,则实数t的取值范围是________.
[-1,0)∪[3,+∞)
分析:设x∈[-4,-2],则x+4∈[0,2],代入[0,2]时f(x)的解析式,再根据f(x+4)=9f(x)求出在[-4,-2]上f(x)的解析式,将f(x)≥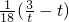 恒成立转化成
恒成立转化成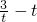 ≤
≤ (x2-6x+8)min=
(x2-6x+8)min= 即可,求出t的取值范围即可.
即可,求出t的取值范围即可.
解答:设x∈[-4,-2],则x+4∈[0,2]
f(x+4)=(x+4)2-2(x+4)=x2-6x+8=3f(x+2)=9f(x)
即f(x)= (x2-6x+8)
(x2-6x+8)
∵f(x)= (x2-6x+8)≥
(x2-6x+8)≥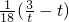 恒成立
恒成立
∴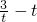 ≤
≤ (x2-6x+8)min=
(x2-6x+8)min=
解得:t∈[-1,0)∪[3,+∞)
故答案为:[-1,0)∪[3,+∞)
点评:本题主要考查了函数最值的应用,以及函数解析式的求解及常用方法,本题解题的关键将区间[-4,-2]转化到区间[0,2],易错在直接代入解析式计算,没有弄清在每一段的函数解析式不一样.
分析:设x∈[-4,-2],则x+4∈[0,2],代入[0,2]时f(x)的解析式,再根据f(x+4)=9f(x)求出在[-4,-2]上f(x)的解析式,将f(x)≥
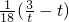 恒成立转化成
恒成立转化成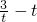 ≤
≤ (x2-6x+8)min=
(x2-6x+8)min= 即可,求出t的取值范围即可.
即可,求出t的取值范围即可.解答:设x∈[-4,-2],则x+4∈[0,2]
f(x+4)=(x+4)2-2(x+4)=x2-6x+8=3f(x+2)=9f(x)
即f(x)=
 (x2-6x+8)
(x2-6x+8)∵f(x)=
 (x2-6x+8)≥
(x2-6x+8)≥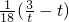 恒成立
恒成立∴
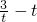 ≤
≤ (x2-6x+8)min=
(x2-6x+8)min=
解得:t∈[-1,0)∪[3,+∞)
故答案为:[-1,0)∪[3,+∞)
点评:本题主要考查了函数最值的应用,以及函数解析式的求解及常用方法,本题解题的关键将区间[-4,-2]转化到区间[0,2],易错在直接代入解析式计算,没有弄清在每一段的函数解析式不一样.

练习册系列答案
相关题目