题目内容
已知sin α<0,tan α>0.
(1)求α角的集合;
(2)求 终边所在的象限;
终边所在的象限;
(3)试判断tan sin
sin cos
cos 的符号.
的符号.
(1)求α角的集合;
(2)求
 终边所在的象限;
终边所在的象限;(3)试判断tan
 sin
sin cos
cos 的符号.
的符号.(1)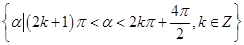
(2)第二、四象限
(3)见解析
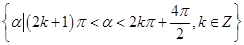
(2)第二、四象限
(3)见解析
解:(1)由sin α<0,
知α在第三、四象限或y轴的负半轴上;
由tan α>0,知α在第一、三象限,
故α角在第三象限,其集合为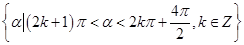 .
.
(2)由(2k+1)π<α<2kπ+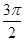 ,
,
得kπ+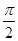 <
< <kπ+
<kπ+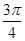 ,k∈Z,
,k∈Z,
故 终边在第二、四象限.
终边在第二、四象限.
(3)当 在第二象限时,
在第二象限时,
tan <0,sin
<0,sin >0,cos
>0,cos <0,
<0,
所以tan sin
sin cos
cos 取正号;
取正号;
当 在第四象限时,
在第四象限时,
tan <0,sin
<0,sin <0,cos
<0,cos >0,
>0,
所以tan sin
sin cos
cos 也取正号.
也取正号.
因此,tan sin
sin cos
cos 取正号.
取正号.
知α在第三、四象限或y轴的负半轴上;
由tan α>0,知α在第一、三象限,
故α角在第三象限,其集合为
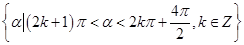 .
.(2)由(2k+1)π<α<2kπ+
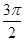 ,
,得kπ+
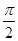 <
< <kπ+
<kπ+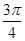 ,k∈Z,
,k∈Z,故
 终边在第二、四象限.
终边在第二、四象限.(3)当
 在第二象限时,
在第二象限时,tan
 <0,sin
<0,sin >0,cos
>0,cos <0,
<0,所以tan
 sin
sin cos
cos 取正号;
取正号;当
 在第四象限时,
在第四象限时,tan
 <0,sin
<0,sin <0,cos
<0,cos >0,
>0,所以tan
 sin
sin cos
cos 也取正号.
也取正号.因此,tan
 sin
sin cos
cos 取正号.
取正号.
练习册系列答案
相关题目
 中,射线OP交单位圆O于点P,若∠XOP =θ,则点P的坐标是( ).
中,射线OP交单位圆O于点P,若∠XOP =θ,则点P的坐标是( ).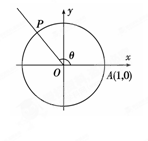
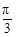 ,k∈Z}
,k∈Z}



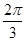 弧长到达Q点,则Q点的坐标为________.
弧长到达Q点,则Q点的坐标为________.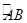 的弧长;
的弧长;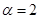 ,则点P
,则点P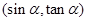 所在的象限是( )
所在的象限是( ) ,
, ,
, ,则( )
,则( )