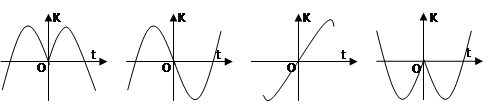题目内容
设 是R上的可导函数,且满足
是R上的可导函数,且满足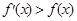 ,对任意的正实数
,对任意的正实数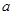 ,下列不等式恒成立的是
,下列不等式恒成立的是
A.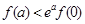 ; ; | B.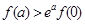 ; ; |
C.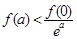 ; ; | D.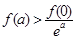 |
B
解析试题分析:构造函数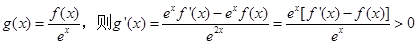 ,即
,即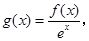 是增函数,而a>0,所以,g(a)>g(0),即
是增函数,而a>0,所以,g(a)>g(0),即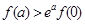 ,关系B。
,关系B。
考点:导数的运算法则,利用导数研究函数的单调性。
点评:小综合题,比较大小问题,往往利用函数的单调性,而利用导数研究函数的单调性,是常用方法。本题关键是构造函数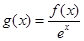 。
。

练习册系列答案
相关题目
若函数 的图象上任意点处切线的倾斜角为
的图象上任意点处切线的倾斜角为 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
由曲线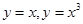 围成的封闭图形面积为[ ]
围成的封闭图形面积为[ ]
A.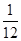 | B.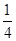 | C.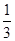 | D.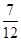 |
若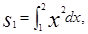
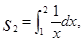
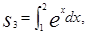 则s1,s2,s3的大小关系为( )
则s1,s2,s3的大小关系为( )
| A.s1<s2<s3 | B.s2<s1<s3 |
| C.s2<s3<s1 | D.s3<s2<s1 |
若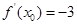 ,则
,则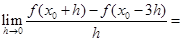 ( )
( )
A.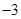 | B.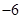 | C.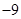 | D.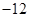 |
已知 是定义在
是定义在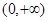 上的非负可导函数,且满足
上的非负可导函数,且满足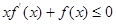 .对任意正数
.对任意正数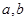 ,若
,若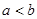 ,则必有( )
,则必有( )
A.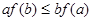 | B.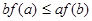 |
C.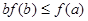 | D.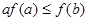 |
函数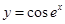 的导数是( )
的导数是( )
A.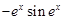 | B.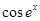 | C.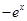 | D.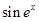 |
已知函数f(x)=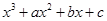 ,下列结论中错误的是( )
,下列结论中错误的是( )
A.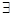 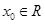 , f( , f(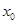 )=0 )=0 |
| B.函数y=f(x)的图像是中心对称图形 |
C.若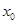 是f(x)的极小值点,则f(x)在区间(-∞, 是f(x)的极小值点,则f(x)在区间(-∞, 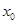 )单调递减 )单调递减 |
D.若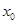 是f(x)的极值点,则 是f(x)的极值点,则  ( (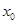 )=0 )=0 |
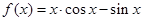 的导函数的部分图象为( )
的导函数的部分图象为( )