题目内容
(本小题满分12分)若函数y=lg(3-4x+x2)的定义域为M.当x∈M时,求f(x)=2x+2-3×4x的最值及相应的x的值.
解:y=lg(3-4x+x2),∴3-4x+x2>0,
解得x<1或x>3,∴M={x|x<1,或x>3}.
f(x)=2x+2-3×4x=4×2x-3×(2x)2.
令2x=t,∵ x<1或x>3,∴t>8或0<t<2.
x<1或x>3,∴t>8或0<t<2.
∴f(x)=4t-3t2=-32+(t>8或0<t<2).
由二次函数性质可知:当0<t<2时,f(x)∈,
当t>8时,f(x)∈(-∞,-160),
当2x=t=,即x=log2时,f(x)=.
综上可知:当x=log2时,f(x)取到最大值为,无最小值.
解得x<1或x>3,∴M={x|x<1,或x>3}.
f(x)=2x+2-3×4x=4×2x-3×(2x)2.
令2x=t,∵
 x<1或x>3,∴t>8或0<t<2.
x<1或x>3,∴t>8或0<t<2.∴f(x)=4t-3t2=-32+(t>8或0<t<2).
由二次函数性质可知:当0<t<2时,f(x)∈,
当t>8时,f(x)∈(-∞,-160),
当2x=t=,即x=log2时,f(x)=.
综上可知:当x=log2时,f(x)取到最大值为,无最小值.
略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 (单位:元)与其重量
(单位:元)与其重量 (单位:克)的平方成正比,且
(单位:克)的平方成正比,且 克该种矿石的价值为
克该种矿石的价值为 元。
元。 的两块矿石,求价值损失的百分率;
的两块矿石,求价值损失的百分率; ;在切割过程中的重量损耗忽略不计)
;在切割过程中的重量损耗忽略不计) 。
。 ,从集合{0,1,2}中任取一个元素作为b,求方程
,从集合{0,1,2}中任取一个元素作为b,求方程 有两个不等实数根的概率;
有两个不等实数根的概率; 中任取一个数作为
中任取一个数作为 ,求方程
,求方程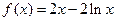

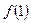 )处的切线方程
)处的切线方程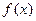 的极值
的极值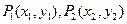 ,如果存在曲线上的点
,如果存在曲线上的点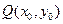 ,且
,且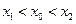 ,使得曲线在点
,使得曲线在点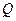 处的切线
处的切线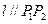 ,则称
,则称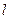 为弦
为弦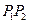 的陪伴切线.已知两点
的陪伴切线.已知两点
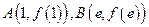 ,试求弦
,试求弦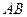 的陪伴切线
的陪伴切线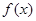 满足
满足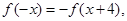 当
当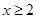 时,
时,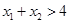 且
且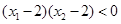 ,则
,则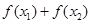 的值为( )
的值为( )
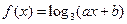 的图象经过点A(2,1)和B(5
的图象经过点A(2,1)和B(5 ,2),记
,2),记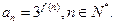
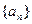 的通项公式;
的通项公式;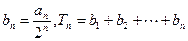 ,若3-
,若3-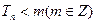 恒成立,求
恒成立,求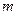 的最小值
的最小值
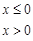 ,若
,若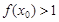 ,则
,则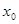 的取值范围是( )
的取值范围是( )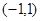



 满足
满足 ,则不等式
,则不等式 的解集是
的解集是  的图象关于直线
的图象关于直线 对称,则实数
对称,则实数 的值为__________________.
的值为__________________.