题目内容
幂函数y1=x-1，y2=x，y3=x
，y4=x3，其中定义域为R且为奇函数有（ ）
| 1 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
分析：考查各个选项中的函数是否满足定义域为R且为奇函数，把满足条件的找出来．
解答：解：函数y1=x-1=
是奇函数，但定义域不是R，不满足条件．
y 2 =x 是奇函数，定义域为R，满足条件． y4 =x3 是奇函数，定义域为R，满足条件．
y3=x
=
是非奇非偶函数，定义域不是R，不满足条件．
综上，满足条件的有2个，
故选C．
| 1 |
| x |
y 2 =x 是奇函数，定义域为R，满足条件． y4 =x3 是奇函数，定义域为R，满足条件．
y3=x
| 1 |
| 2 |
| x |
综上，满足条件的有2个，
故选C．
点评：本题考查函数的定义域，函数的奇偶性的判断方法．
练习册系列答案
相关题目
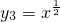，y4=x3，其中定义域为R且为奇函数有
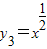，y4=x3，其中定义域为R且为奇函数有（ ）