题目内容
三角不等式组
|
分析:由题意,先将三角不等式组
变为
,再由正切函数的性质与余弦函数的性质求出不等式组的解集即可得到正确答案
|
|
解答:解:由已知,三角不等式组
变为
,
由tanx<1得-
+kπ<x<
+kπ,k∈z
由cosx≥
,或cosx≤-
解得2kπ-
<x<2kπ+
(k∈Z)或2kπ+
<x<2kπ+
(k∈Z),即kπ-
<x<kπ+
(k∈Z)
综上知三角不等式组
的解集是[kπ-
,kπ+
](k∈Z)
故答案为[kπ-
,kπ+
](k∈Z)
|
|
由tanx<1得-
| π |
| 2 |
| π |
| 4 |
由cosx≥
| ||
| 2 |
| ||
| 2 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| 4π |
| 3 |
| π |
| 6 |
| π |
| 6 |
综上知三角不等式组
|
| π |
| 6 |
| π |
| 6 |
故答案为[kπ-
| π |
| 6 |
| π |
| 6 |
点评:本题考查正切函数的单调性,解答本题关键是熟练掌握正切函数与余弦函数的单调性且能根据性质解三角不等式,近几年高考中三角不等式解法一般出现在求三角函数定义域的题型中,所占分比不高,但出现频率较高,学习时对这样的常考的知识点应牢固掌握好好领会

练习册系列答案
相关题目
 >0;
>0; .
.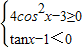 的解集是 .
的解集是 .