题目内容
已知数列{an} 满足a1=a，且a n+1=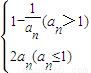
，对任意的n∈N*，总有a n+3=an成立，则a在（0，1]内的可能值有（ ）A．1个
B．2个
C．3个
D．4个
【答案】分析：a1=a∈（0，1]，a2=2a，若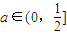
，a2=2a∈（0，1]，a3=4a，
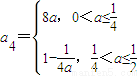．由此能求出
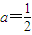，若
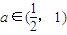，a2=2a∈（1，2]，
，
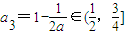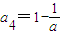．由此能求出a=1．
解答：解：a1=a∈（0，1]，a2=2a，
①若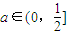
，a2=2a∈（0，1]，
a3=4a，
．
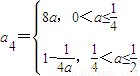由a4=a1=a得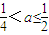
，
且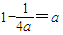
，
故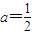
，此时经检验对任意的n∈N*，总有an+3=an．
②若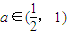
，
a2=2a∈（1，2]，
，
．
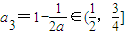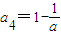由a4=a1=a得a=1，此时经检验对任意的n∈N*，总有an+3=an．
故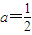
或a=1．
故选B．
点评：本题考查数列的递推式的应用，解题时要认真审题，注意分类讨论思想的灵活运用．
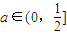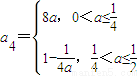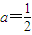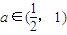，a2=2a∈（0，1]，a3=4a，．由此能求出，若，a2=2a∈（1，2]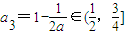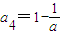，，．由此能求出a=1．解答：解：a1=a∈（0，1]，a2=2a，
①若
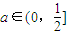，a2=2a∈（0，1]，a3=4a，
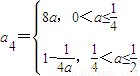．由a4=a1=a得
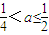，且
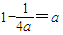，故
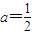，此时经检验对任意的n∈N*，总有an+3=an．②若
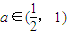，a2=2a∈（1，2]，
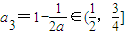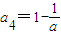，．由a4=a1=a得a=1，此时经检验对任意的n∈N*，总有an+3=an．
故
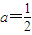或a=1．故选B．
点评：本题考查数列的递推式的应用，解题时要认真审题，注意分类讨论思想的灵活运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目