题目内容
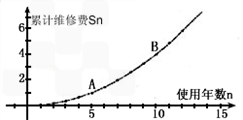
现在汽车是很给力的,汽车生产商对某款汽车的维修费进行电脑模拟实验,分别以汽车年数n和前n年累计维修费sn(万元)为横、纵坐标,发现点(n,sn)在函数y=ax2+bx(a≠0)的图象上,其中图象上两点A(5,1.05),B(10,4.1).
(1)求出累计维修费sn关于使用年数n的表达式,并求出第n年的维修费;
(2)汽车开始使用后每年需维修,按国家质量标准规定,出售后前两年作为保修时间,此时间段由产家承担维修费,保修期过后,汽车维修费有车主承担.若某人以9.18万元购买这款汽车,求年平均耗资费的最小值.(耗资费=购买费+车主承担的维修费)
(1)求出累计维修费sn关于使用年数n的表达式,并求出第n年的维修费;
(2)汽车开始使用后每年需维修,按国家质量标准规定,出售后前两年作为保修时间,此时间段由产家承担维修费,保修期过后,汽车维修费有车主承担.若某人以9.18万元购买这款汽车,求年平均耗资费的最小值.(耗资费=购买费+车主承担的维修费)
分析:(1)根据函数y=ax2+bx(a≠0)的图象上两点A(5,1.05),B(10,4.1),可求函数的关系式,进而可得维修费Sn关于使用年数n的表达式,从而可求出第n年的维修费;
(2)根据耗资费=购买费+车主承担的维修费,可得年平均耗资费,利用基本不等式,可求其最小值.
(2)根据耗资费=购买费+车主承担的维修费,可得年平均耗资费,利用基本不等式,可求其最小值.
解答:解:(1)由题意,函数y=ax2+bx(a≠0)的图象上两点A(5,1.05),B(10,4.1),
∴1.05=25a+5b,4.1=100a+10b
∴a=
,b=
∵点(n,Sn)在函数y=ax2+bx(a≠0)的图象上,
∴Sn=
n2+
n
n≥2时,an=Sn-Sn-1=
n-
,n=1时,a1=S1=
也满足上式
∴第n年的维修费为an=
n-
;
(2)∵耗资费=购买费+车主承担的维修费
∴年平均耗资费为y=
=0.04n+
+0.01≥1.21(万元)
当且仅当n=15时取等号
∴年平均耗资费的最小值为1.21万元.
∴1.05=25a+5b,4.1=100a+10b
∴a=
| 1 |
| 25 |
| 1 |
| 100 |
∵点(n,Sn)在函数y=ax2+bx(a≠0)的图象上,
∴Sn=
| 1 |
| 25 |
| 1 |
| 100 |
n≥2时,an=Sn-Sn-1=
| 2 |
| 25 |
| 3 |
| 100 |
| 1 |
| 20 |
∴第n年的维修费为an=
| 2 |
| 25 |
| 3 |
| 100 |
(2)∵耗资费=购买费+车主承担的维修费
∴年平均耗资费为y=
| 9.18+a3+a4+…+an |
| n |
| 9 |
| n |
当且仅当n=15时取等号
∴年平均耗资费的最小值为1.21万元.
点评:本题考查数列与函数的综合,考查数列的运用,考查利用基本不等式求最值,解题的关键是确定函数关系式.

练习册系列答案
相关题目
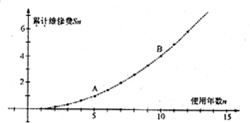 现在“汽车”是很“给力”的名词.汽车厂商对某款汽车的维修费进行电脑模拟试验,分别以汽车使用年限n和前n年累计维修费Sn(万元)为横、纵坐标绘制成点,发现点(n,Sn)在函数y=ax2+bx(a≠0)的图象上(如图所示),其中A(5,1.05)、B(10,4.1).
现在“汽车”是很“给力”的名词.汽车厂商对某款汽车的维修费进行电脑模拟试验,分别以汽车使用年限n和前n年累计维修费Sn(万元)为横、纵坐标绘制成点,发现点(n,Sn)在函数y=ax2+bx(a≠0)的图象上(如图所示),其中A(5,1.05)、B(10,4.1). )
)