题目内容
12．在平面直角坐标系xOy中，点A（-1，0），$B（\;0\;，\;\sqrt{3}\;）$，C（cosx，sinx），则$\overrightarrow{AB}$=$（1，\sqrt{3}）$；若$\overrightarrow{AB}$∥$\overrightarrow{OC}$，则tanx=$\sqrt{3}$．分析 直接利用向量的坐标运算求解第一个空；利用向量的共线求解第二个空．
解答 解：在平面直角坐标系xOy中，点A（-1，0），$B（\;0\;，\;\sqrt{3}\;）$，C（cosx，sinx），
则$\overrightarrow{AB}$=$（1，\sqrt{3}）$；
$\overrightarrow{AB}$∥$\overrightarrow{OC}$，可得：sinx=$\sqrt{3}$cosx，
可得tanx=$\sqrt{3}$．
故答案为：$（1，\sqrt{3}）$；$\sqrt{3}$
点评 本题考查向量的坐标运算以及向量共线充要条件的应用，基本知识的考查．
练习册系列答案
相关题目
2．某流程图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
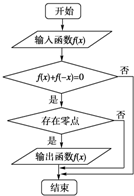
| A． | f（x）=$\frac{{2}^{x}-1}{{2}^{x}+1}$ | B． | f（x）=$\frac{cosx}{x}$（-$\frac{π}{2}$$＜x＜\frac{π}{2}$） | ||
| C． | f（x）=$\frac{|x|}{x}$ | D． | f（x）=x2ln（x2+1） |
3．双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的渐近线方程是（ ）
| A． | y=±$\frac{2}{3}$x | B． | y=±$\frac{4}{9}$x | C． | y=±$\frac{3}{2}$x | D． | y=±$\frac{9}{4}$x |
7．当n=5时，执行如图所示的程序框图，输出的S值是（ ）
| A． | 7 | B． | 10 | C． | 11 | D． | 16 |
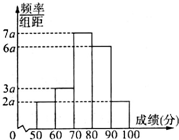100名学生某次数学测试成绩（单位：分）的频率分布直方图如图所示，则模块测试成绩落在[50，70）中的学生人数是25．
为了考查某厂2000名工人的生产技能情况，随机抽查了该厂n名工人某天的产量（单位：件），整理后得到如下的频率分布直方图（产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35]），其中产量在[20，25）的工人有6名．