题目内容
3.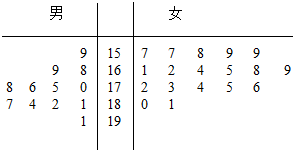 第4届湘台经贸洽谈交流会于2011年6月在我市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.(I)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?(Ⅱ)若从所有“高个子”中选3名志愿者,用X表示所选志愿者中能担任“礼仪小姐”的人数,试写出X的分布列,并求X的数学期望.
第4届湘台经贸洽谈交流会于2011年6月在我市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.(I)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?(Ⅱ)若从所有“高个子”中选3名志愿者,用X表示所选志愿者中能担任“礼仪小姐”的人数,试写出X的分布列,并求X的数学期望.
分析 (I)由题意及茎叶图,有“高个子”12人,“非高个子”18人,利用用分层抽样的方法,每个人被抽中的概率是$\frac{5}{30}$=$\frac{1}{6}$,利用对立事件即可;
(Ⅱ)由于从所有“高个子”中选3名志愿者,用ξ表示所选志愿者中能担任“礼仪小姐”的人数,利用离散型随机变量的定义及题意可知ξ的取值为0,1,2,3在利用古典概型的概率公式求出每一个值对应事件的概率,有期望的公式求出即可.
解答 解:(I)根据茎叶图,有“高个子”12人,“非高个子”18人,
用分层抽样的方法,每个人被抽中的概率是$\frac{5}{30}$=$\frac{1}{6}$,
所以选中的“高个子”有12×=2人,“非高个子”有18×$\frac{1}{6}$=3人.
用事件A表示“至少有一名“高个子”被选中”,
则它的对立事件A?表示“没有一名“高个子”被选中”,
则P(A)=1-$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{710}{\;}$.
因此,至少有一人是“高个子”的概率是$\frac{7}{10}$.
(Ⅱ)依题意,X的取值为0,1,2,3.
P(X=0)=$\frac{{C}_{8}^{3}}{{C}_{12}^{3}}$=$\frac{14}{55}$,P(X=1)=$\frac{{C}_{4}^{1}{C}_{8}^{2}}{{C}_{12}^{3}}$=$\frac{28}{55}$,
P(X=2)=$\frac{{C}_{4}^{2}{C}_{8}^{1}}{{C}_{12}^{3}}$=$\frac{12}{55}$,P(X=3)=$\frac{{C}_{4}^{3}}{{C}_{12}^{3}}$=$\frac{1}{55}$.
因此,X的分布列如下:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{14}{55}$ | $\frac{28}{55}$ | $\frac{12}{55}$ | $\frac{1}{55}$ |
点评 本题主要考查茎叶图、分层抽样、随机事件的概率、对立事件的概率、随机变量的分布列以及数学期望等基础知识,考查运用概率统计知识解决简单实际问题的数据处理能力和应用意识.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案| A. | sinα | B. | -sinα | C. | cosα | D. | -cosα |
| A. | $\frac{9}{25}$ | B. | $\frac{4}{25}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
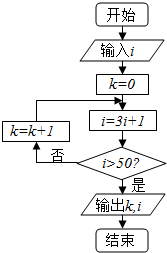
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| 评分 | 1 | 2 | 3 | 4 | 5 |
| 人数 | x | 20 | 10 | 5 | y |
(Ⅰ)求x与y的值;
(Ⅱ)若将频率视为概率,现从对该商品作出了评价的顾客中,随机抽取一位,记该顾客的评分为X,求随机变量X的分布列一与数学期望.