题目内容
15.方程log2(3x+2)=1+log2(x+2)的解为2.分析 直接利用对数运算法则化简求解方程的解即可.
解答 解:方程log2(3x+2)=1+log2(x+2),可得log2(3x+2)=log2(2x+4),
可得3x+2=2x+4,解得x=2,
经检验可知x=2是方程的解.
故答案为:2.
点评 本题考查对数方程的解法,注意方程根的检验.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
6.如图,正方体ABCD-A′B′C′D′中,AB的中点为E,AA′的中点为F,则直线D′F和直线CE( )
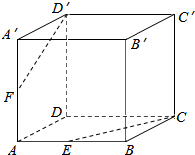

| A. | 都与直线DA相交,且交于同一点 | B. | 互相平行 | ||
| C. | 异面 | D. | 都与直线DA相交,但交于不同点 |
3.四面体ABCD中,∠CBD=90°,AB⊥面BCD,点E、F分别为BC、CD的中点,过点E、F和四面体ABCD的外接球球心O的平面将四面体ABCD分成两部分,则较小部分的体积与四面体ABCD的体积之比为( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{27}{64}$ |
10.以下关于函数f(x)=$\frac{2x-1}{x-3}$(x≠3)的叙述正确的是( )
| A. | 函数f(x)在定义域内有最值 | |
| B. | 函数f(x)在定义域内单调递增 | |
| C. | 函数f(x)的图象关于点(3,1)对称 | |
| D. | 函数y=$\frac{5}{x}$的图象朝右平移3个单位再朝上平移2个单位即得函数f(x) |
20.从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知 P(A)=0.65,P(B)=0.2,P(C)=0.1.则事件“抽到的不是二等品”的概率为( )
| A. | 0.75 | B. | 0.25 | C. | 0.8 | D. | 0.2 |
4.函数f(x)=ex+2x-4的零点所在的区间是( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | (1,$\frac{3}{2}$) |