题目内容
 抛物线y=b(
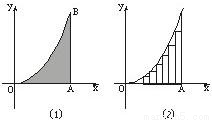
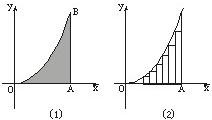
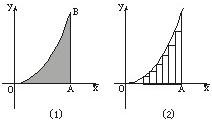
抛物线y=b( )2、x轴及直线AB:x=a围成了如图(1)的阴影部分,AB与x轴交于点A,把线段OA分成n等份,作以
)2、x轴及直线AB:x=a围成了如图(1)的阴影部分,AB与x轴交于点A,把线段OA分成n等份,作以 为底的内接矩形如图(2),阴影部分的面积为S等于这些内接矩形面积之和当n→∞时的极限值,求S.
为底的内接矩形如图(2),阴影部分的面积为S等于这些内接矩形面积之和当n→∞时的极限值,求S.
解:因为把线段OA分成n等份,作以 为底的内接矩形,
为底的内接矩形,
所以S= [b•(
[b•( )2+b•(
)2+b•( )2+b•(
)2+b•(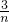 )2++b•(
)2++b•( )2]2•
)2]2•
=
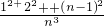 •ab
•ab
=
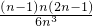 •ab
•ab
= ab.
ab.
分析:首先分析题目把阴影部分分成n个小矩形,当n→∞时这些内接矩形面积之和的极限值为阴影部分面积,又已知内接矩形的底和高,故可以列出内接矩形的面积和,然后化简求得极限即可得到答案.
点评:此题主要考查极限及其运算问题,题目看似较复杂,但考查的都是基本的内容.求出内接矩形面积之和是解题的关键,有一定的计算量属于中档题目.
 为底的内接矩形,
为底的内接矩形,所以S=
 [b•(
[b•( )2+b•(
)2+b•( )2+b•(
)2+b•(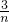 )2++b•(
)2++b•( )2]2•
)2]2•
=

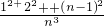 •ab
•ab=

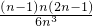 •ab
•ab=
 ab.
ab.分析:首先分析题目把阴影部分分成n个小矩形,当n→∞时这些内接矩形面积之和的极限值为阴影部分面积,又已知内接矩形的底和高,故可以列出内接矩形的面积和,然后化简求得极限即可得到答案.
点评:此题主要考查极限及其运算问题,题目看似较复杂,但考查的都是基本的内容.求出内接矩形面积之和是解题的关键,有一定的计算量属于中档题目.

练习册系列答案
相关题目
 抛物线y=b(
抛物线y=b(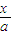 )2、x轴及直线AB:x=a围成了如图(1)的阴影部分,AB与x轴交于点A,把线段OA分成n等份,作以
)2、x轴及直线AB:x=a围成了如图(1)的阴影部分,AB与x轴交于点A,把线段OA分成n等份,作以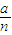 为底的内接矩形如图(2),阴影部分的面积为S等于这些内接矩形面积之和当n→∞时的极限值,求S.
为底的内接矩形如图(2),阴影部分的面积为S等于这些内接矩形面积之和当n→∞时的极限值,求S.