题目内容
设P(x1,y1),Q(x2,y2)为椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
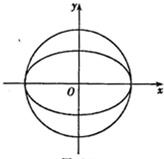
(1)如图,若向圆O内随机投一点A,点A落在椭圆C的概率为
| 1 |
| 2 |
| 3 |
(i)求椭圆C的标准方程;
(ii)若点B(0,1)且
| QB |
| OP |
(2)若直线OP和OQ的斜率之积为
| b2 |
| a2 |
分析:(1)(i)由已知得
,又a2=b2+c2,由此能得到椭圆C的方程.
(ii)由
=
,得(-x2,1-y2)=(x1,y1),所以
,结合圆的对称性知点P,Q关于y轴对称且PQ的中点坐标为(0,
),由此能求出直线OP的斜率.
(2)设OP方程为y=kx,代入
+
=1,得x12=
,由kOP•koQ=
,得x22=
=
,所以x12+x22=
+
=a2,由此知点M(x1,x2)在圆O:x2+y2=a2上.
|
(ii)由
| QB |
| OP |
|
| 1 |
| 2 |
(2)设OP方程为y=kx,代入
| x2 |
| a2 |
| y2 |
| b2 |
| a2b2 |
| a2k2+b2 |
| b2 |
| a2 |
| a2b2 | ||
a2(
|
| a2k2 |
| a2k2+b2 |
| a2b2 |
| a2k2+b2 |
| a4k2 |
| a2k2 +b2 |
解答:解:(1)(i)由已知得
,又a2=b2+c2,解得a=2,b=1,
∴椭圆C的方程为
+y2=1.
(ii)由
=
,得(-x2,1-y2)=(x1,y1),
∴
,
结合圆的对称性知点P,Q关于y轴对称且PQ的中点坐标为(0,
),
故直线PQ的方程为y=
,从而得p(±
,
),
∴kOP=
=±
.
(2)由题意知直线OP的斜率存在,设其方程为y=kx,
代入
+
=1,整理,得x12=
①
由kOP•koQ=
,用
代替①中的k,得
x22=
=
,
∴x12+x22=
+
=a2,
∴点M(x1,x2)在圆O:x2+y2=a2上.
|
∴椭圆C的方程为
| x2 |
| 4 |
(ii)由
| QB |
| OP |
∴
|
结合圆的对称性知点P,Q关于y轴对称且PQ的中点坐标为(0,
| 1 |
| 2 |
故直线PQ的方程为y=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
∴kOP=
| ||
±
|
| ||
| 6 |
(2)由题意知直线OP的斜率存在,设其方程为y=kx,
代入
| x2 |
| a2 |
| y2 |
| b2 |
| a2b2 |
| a2k2+b2 |
由kOP•koQ=
| b2 |
| a2 |
| b2 |
| a2k |
x22=
| a2b2 | ||
a2(
|
| a2k2 |
| a2k2+b2 |
∴x12+x22=
| a2b2 |
| a2k2+b2 |
| a4k2 |
| a2k2 +b2 |
∴点M(x1,x2)在圆O:x2+y2=a2上.
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
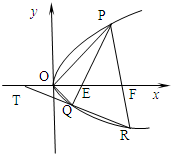 设P(x1,y1),Q(x2,y2) 是抛物线C:y2=2px(p>0)上相异两点,且
设P(x1,y1),Q(x2,y2) 是抛物线C:y2=2px(p>0)上相异两点,且