Question

【题目】已知函数.

（1）若，求函数的值域；

（2）讨论函数的奇偶性，并说明理由.

Answer 1

【答案】（1）； （2）当时，函数为偶函数；当 时，函数是奇函数；当 且 ，函数既不是奇函数，也不是偶函数．.

【解析】

（1）将代入函数解析式，求得函数的定义域，将函数解析式化简，之后借助于指数函数的值域以及不等式的性质求得结果；

（2）分类讨论，利用奇偶函数的定义，讨论函数的奇偶性，从而求得结果.

（1）当 时，定义域为，，

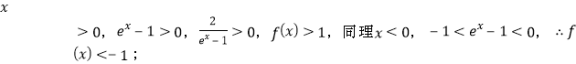
所以值域为 　

（2）①当时，定义域为R，故函数为偶函数；

②当且时，定义域为不关于原点对称，故函数既不是奇函数，也不是偶函数 ；

③当时，定义域为 故函数是奇函数；

④当时，定义域为R关于原点对称，若是奇函数

当时，故函数是奇函数；

若是偶函数

且时，，函数既不是奇函数，也不是偶函数．

综上：

当时，函数为偶函数；

当 时，函数是奇函数；

当 且 ，函数既不是奇函数，也不是偶函数．