题目内容
某中学有5名体育类考生要到某大学参加体育专业测试,学校指派一名老师带队,已知每位考生测试合格的概率均为
.
(Ⅰ)若他们随机坐在所乘坐的汽车的前后两排各三个座位上,求体育老师不坐后排的概率;
(Ⅱ)若5人中恰有r人合格的概率为
,求r的值.
| 2 |
| 3 |
(Ⅰ)若他们随机坐在所乘坐的汽车的前后两排各三个座位上,求体育老师不坐后排的概率;
(Ⅱ)若5人中恰有r人合格的概率为
| 80 |
| 243 |
分析:(Ⅰ)根据体育老师的坐法共有3+3=6种,不坐后排的坐法共有3种,求出体育老师不坐后排的概率为
.
(Ⅱ)由题意可得,5人中恰有r人合格的概率
(
)r•(
)5-r=
,解方程求得r的值.
| 3 |
| 6 |
(Ⅱ)由题意可得,5人中恰有r人合格的概率
| C | r 5 |
| 2 |
| 3 |
| 1 |
| 3 |
| 80 |
| 243 |
解答:解:(Ⅰ)体育老师的坐法共有3+3=6种,不坐后排的坐法共有3种,
故体育老师不坐后排的概率为
=
.…(5分)
(Ⅱ)5人中恰有r人合格的概率
(
)r•(
)5-r.…(7分)
由题意可得
(
)r•(
)5-r=
,即C5r•2r=80.
解得r=3或4.…(12分)
故体育老师不坐后排的概率为
| 3 |
| 6 |
| 1 |
| 2 |
(Ⅱ)5人中恰有r人合格的概率
| C | r 5 |
| 2 |
| 3 |
| 1 |
| 3 |
由题意可得
| C | r 5 |
| 2 |
| 3 |
| 1 |
| 3 |
| 80 |
| 243 |
解得r=3或4.…(12分)
点评:本题主要考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,得到
(
)r•(
)5-r=
,是解题的关键.
| C | r 5 |
| 2 |
| 3 |
| 1 |
| 3 |
| 80 |
| 243 |

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 .
.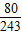 ,求r的值.
,求r的值.