题目内容

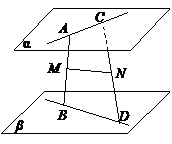
设平面α∥β，两条异面直线AC和BD分别在平面α、β内，线段AB、CD中点分别为M、N，设MN=a，线段AC=BD=2a，求异面直线AC和BD所成的角.

600


解析:

连接AD,取AD中点P,连接PM、PN，

    则PN∥AC，PM∥BD，

且 

   

∴∠MPN即是异面直线AC和BD所成的角，

    又∵MN=，∴ΔPMN是等边三角形

∴∠MPN=600

∴异面直线AC和BD所成的角为600

练习册系列答案
相关题目
6、设ab是两条异面直线，P是ab外的一点，则下列结论正确的是（　　）
7、设m，n为两条直线，α，β为两个平面，则下列四个命题中，正确的命题是（　　）
9、给出命题：
（1）在空间里，垂直于同一平面的两个平面平行；
（2）设l，m是不同的直线，α是一个平面，若l⊥α，l∥m，则m⊥α；
（3）已知α，β表示两个不同平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的充要条件；
（4）a，b是两条异面直线，P为空间一点，过P总可以作一个平面与a，b之一垂直，与另一个平行．
其中正确命题个数是（　　）
在平面直角坐标系xOy中，已知⊙C1：（x+3）2+（y-1）2=4和⊙C2：（x-5）2+（y-1）2=4
（1）若直线l过点O（0，0），且被⊙C1截得的弦长为2
3
，求直线l的方程；
（2）设P为平面上的点，满足：过点P的任意互相垂直的直线l1和l2，只要l1和l2与⊙C1和⊙C2分别相交，必有直线l1被⊙C1截得的弦长与直线l2被⊙C2截得的弦长相等，试求所有满足条件的点P的坐标；
（3）将（2）的直线l1和l2互相垂直改为直线l1和l2所成的角为60°，其余条件不变，直接写出所有这样的点P的坐标．（直线与直线所成的角与两条异面直线所成的角类似，只取较小的角度．）
设a，b是平面α 外的两条直线，给出下列四个命题：
①若a∥b，a∥α，则b∥α；
②若a∥b，b 与α相交，则a 与α 也相交；
③若a∥α，b∥α，则a∥b；
④若a 与b 异面，a∥α，则b∥α．
则所有正确命题的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网