题目内容
定义在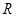 上的函数
上的函数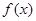 同时满足性质:①对任何
同时满足性质:①对任何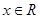 ,均有
,均有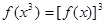 成立;②对任何
成立;②对任何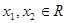 ,当且仅当
,当且仅当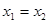 时,有
时,有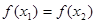 .则
.则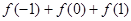 的值为 .
的值为 .
0
解析试题分析:首先根据题干条件解得f(0),f(-1)和f(-1)的值,然后根据对任何x1,x2∈R,x1≠x2均有f(x1)≠f(x2)可以判断f(0)、f(-1)和f(1)不能相等,据此解得答案解:∵对任何x∈R均有f(x3)=[f(x)]3,∴f(0)=(f(0))3,解得f(0)=0,1或-1, f(-1)=(f(-1))3,解得f(-1)=0,1或-1, f(1)=(f(1))3,解得f(1)=0,1或-1,∵对任何x1,x2∈R,x1≠x2均有f(x1)≠f(x2),∴f(0)、f(-1)和f(1)的值只能是0、-1和1中的一个,∴f(0)+f(-1)+f(1)=0,故答案为0
考点:函数的值
点评:本题主要考查函数的值的知识点,解答本题的关键是根据题干条件判断f(0)、f(-1)和f(1)不能相等,本题很容易出错

练习册系列答案
相关题目
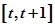 上满足不等式
上满足不等式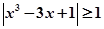 的解有且只有一个,则实数
的解有且只有一个,则实数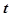 的取值范围是_________。
的取值范围是_________。 的值为 .
的值为 .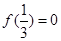 ,则不等式
,则不等式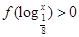 的解集是
的解集是  且函数
且函数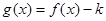 恰有两个零点,则实数
恰有两个零点,则实数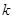 的取值范围是 .
的取值范围是 .  为一次函数,且
为一次函数,且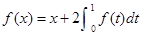 ,则
,则 有负数根,则实数
有负数根,则实数 的取值范围是 .
的取值范围是 . 的定义域为M,
的定义域为M, 的定义域为N,则
的定义域为N,则 =______.
=______. 在区间
在区间 上有解,则所有满足条件的
上有解,则所有满足条件的 的值之和为
的值之和为